Question Number 123133 by Khalmohmmad last updated on 23/Nov/20
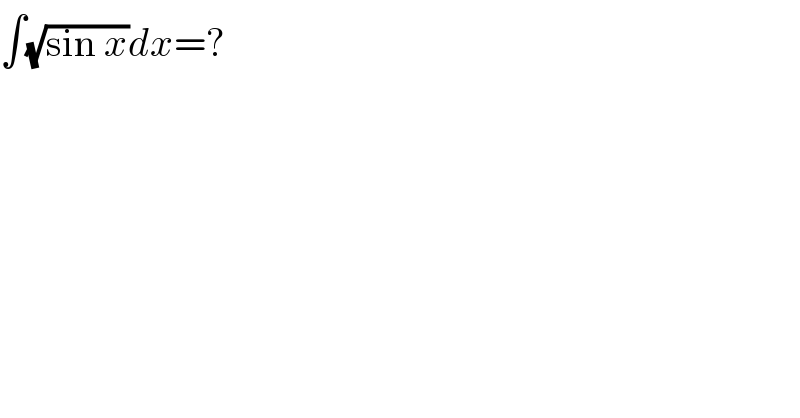
$$\int\sqrt{\mathrm{sin}\:{x}}{dx}=? \\ $$
Commented by MJS_new last updated on 23/Nov/20

$$\mathrm{see}\:\mathrm{question}\:\mathrm{84607} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Nov/20
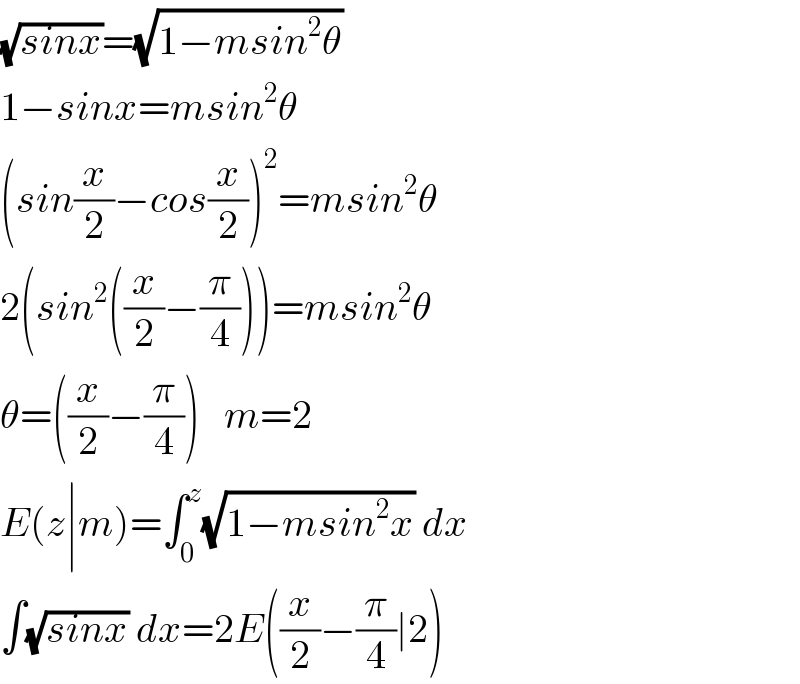
$$\sqrt{{sinx}}=\sqrt{\mathrm{1}−{msin}^{\mathrm{2}} \theta} \\ $$$$\mathrm{1}−{sinx}={msin}^{\mathrm{2}} \theta \\ $$$$\left({sin}\frac{{x}}{\mathrm{2}}−{cos}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} ={msin}^{\mathrm{2}} \theta \\ $$$$\mathrm{2}\left({sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)\right)={msin}^{\mathrm{2}} \theta\:\:\:\:\: \\ $$$$\theta=\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)\:\:\:{m}=\mathrm{2} \\ $$$${E}\left({z}\mid{m}\right)=\int_{\mathrm{0}} ^{{z}} \sqrt{\mathrm{1}−{msin}^{\mathrm{2}} {x}}\:{dx} \\ $$$$\int\sqrt{{sinx}}\:{dx}=\mathrm{2}{E}\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\mid\mathrm{2}\right) \\ $$
