Menu Close

sin-x-dx-6-sin-2-x-

Tinku Tara 0 Comments
Pin




Question Number 105983 by bemath last updated on 02/Aug/20
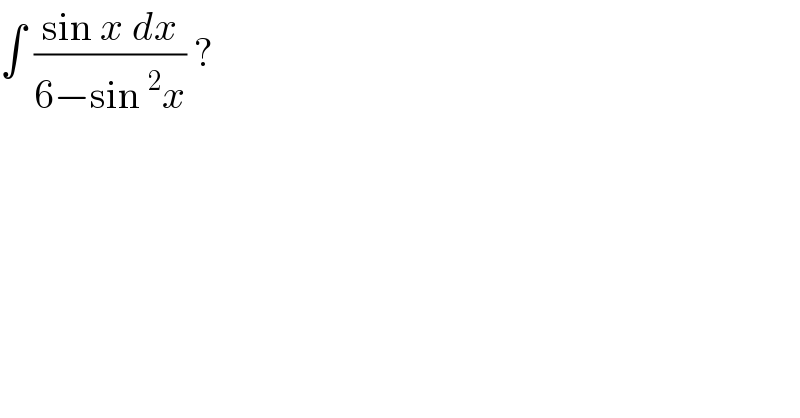
∫ ((sin x dx)/(6−sin^2 x)) ?
$$\int\:\frac{\mathrm{sin}\:{x}\:{dx}}{\mathrm{6}−\mathrm{sin}\:^{\mathrm{2}} {x}}\:?\:\: \\ $$
Commented by bemath last updated on 02/Aug/20
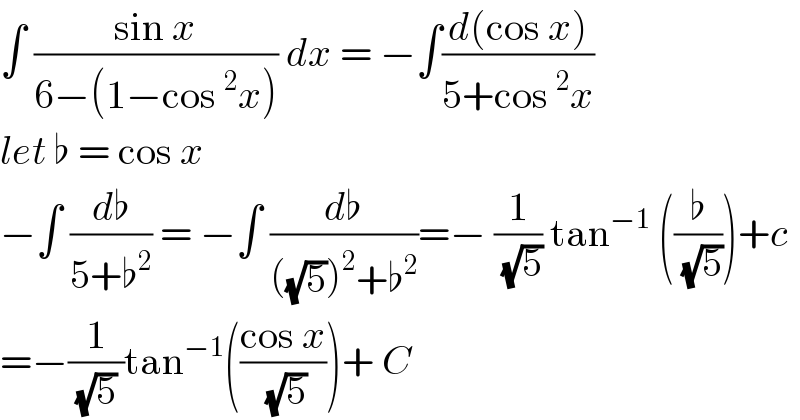
∫ ((sin x)/(6−(1−cos^2 x))) dx = −∫((d(cos x))/(5+cos^2 x)) let ♭ = cos x −∫ (d♭/(5+♭^2 )) = −∫ (d♭/(((√5))^2 +♭^2 ))=− (1/( (√5))) tan^(−1) ((♭/( (√5))))+c =−(1/( (√5) ))tan^(−1) (((cos x)/( (√5))))+ C
$$\int\:\frac{\mathrm{sin}\:{x}}{\mathrm{6}−\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)}\:{dx}\:=\:−\int\frac{{d}\left(\mathrm{cos}\:{x}\right)}{\mathrm{5}+\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$$${let}\:\flat\:=\:\mathrm{cos}\:{x} \\ $$$$−\int\:\frac{{d}\flat}{\mathrm{5}+\flat^{\mathrm{2}} }\:=\:−\int\:\frac{{d}\flat}{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} +\flat^{\mathrm{2}} }=−\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\flat}{\:\sqrt{\mathrm{5}}}\right)+{c} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}\:}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{5}}}\right)+\:{C}\: \\ $$
Answered by Muhsang S L last updated on 02/Aug/20
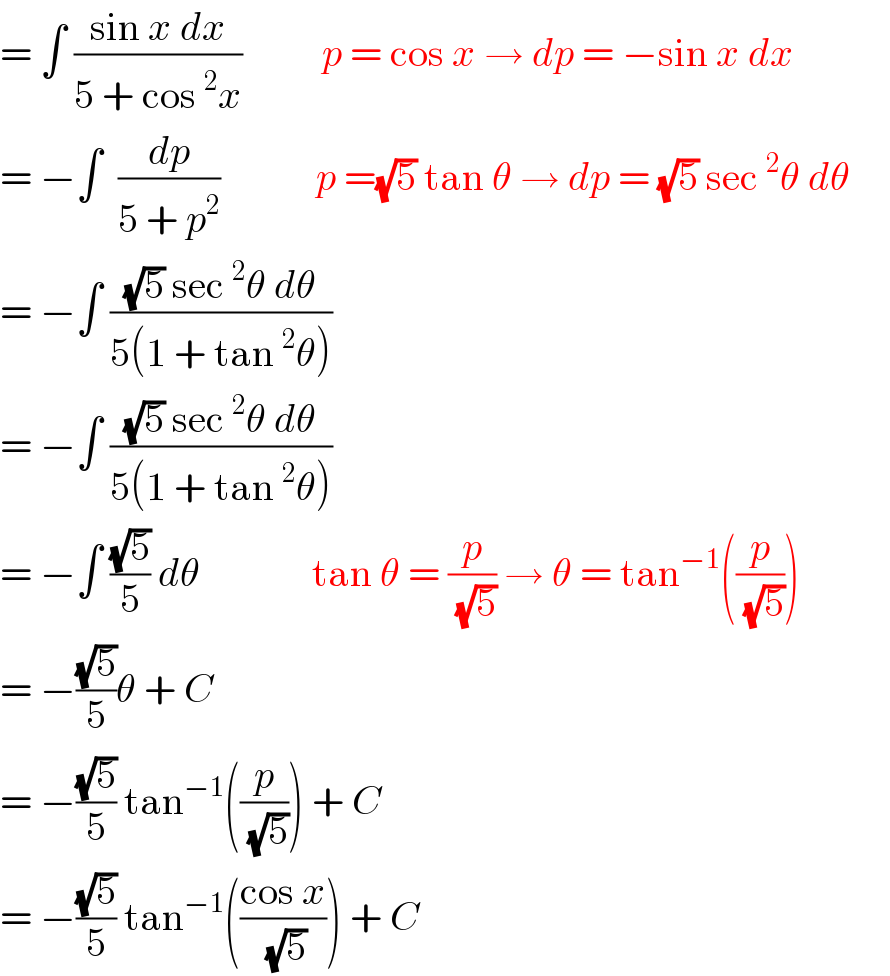
= ∫ ((sin x dx)/(5 + cos^2 x)) p = cos x → dp = −sin x dx = −∫ (dp/(5 + p^2 )) p =(√5) tan θ → dp = (√5) sec^2 θ dθ = −∫ (((√5) sec^2 θ dθ)/(5(1 + tan^2 θ))) = −∫ (((√5) sec^2 θ dθ)/(5(1 + tan^2 θ))) = −∫ ((√5)/5) dθ tan θ = (p/( (√5))) → θ = tan^(−1) ((p/( (√5)))) = −((√5)/5)θ + C = −((√5)/5) tan^(−1) ((p/( (√5)))) + C = −((√5)/5) tan^(−1) (((cos x)/( (√5)))) + C
$$=\:\int\:\frac{\mathrm{sin}\:{x}\:{dx}}{\mathrm{5}\:+\:\mathrm{cos}\:^{\mathrm{2}} {x}}\:\:\:\:\:\:\:\:\:\:{p}\:=\:\mathrm{cos}\:{x}\:\rightarrow\:{dp}\:=\:−\mathrm{sin}\:{x}\:{dx} \\ $$$$=\:−\int\:\:\frac{{dp}}{\mathrm{5}\:+\:{p}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:{p}\:=\sqrt{\mathrm{5}}\:\mathrm{tan}\:\theta\:\rightarrow\:{dp}\:=\:\sqrt{\mathrm{5}}\:\mathrm{sec}\:^{\mathrm{2}} \theta\:{d}\theta\:\:\:\:\: \\ $$$$=\:−\int\:\frac{\sqrt{\mathrm{5}}\:\mathrm{sec}\:^{\mathrm{2}} \theta\:{d}\theta}{\mathrm{5}\left(\mathrm{1}\:+\:\mathrm{tan}\:^{\mathrm{2}} \theta\right)} \\ $$$$=\:−\int\:\frac{\sqrt{\mathrm{5}}\:\mathrm{sec}\:^{\mathrm{2}} \theta\:{d}\theta}{\mathrm{5}\left(\mathrm{1}\:+\:\mathrm{tan}\:^{\mathrm{2}} \theta\right)} \\ $$$$=\:−\int\:\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:{d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{{p}}{\:\sqrt{\mathrm{5}}}\:\rightarrow\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{p}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$=\:−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\theta\:+\:{C} \\ $$$$=\:−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{p}}{\:\sqrt{\mathrm{5}}}\right)\:+\:{C} \\ $$$$=\:−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{5}}}\right)\:+\:{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *