sin-x-pi-2-1-x-2-dx-By-real-analysis-

Question Number 102121 by Rohit@Thakur last updated on 06/Jul/20

\int_{- \infty}^{\infty} \frac{s i n (x + \frac{π}{2})}{1 + x^{2}} d x B y r e a l a n a l y s i s

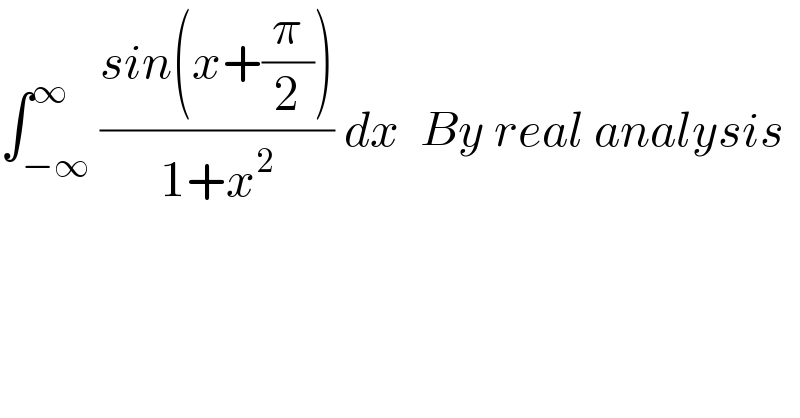
Commented by prakash jain last updated on 06/Jul/20

https://youtu.be/YWBdwYr6PGg Solution video.

Answered by Ar Brandon last updated on 06/Jul/20

Let f (x) = \int_{- \infty}^{\infty} \frac{s i n (x + \frac{π}{2})}{1 + x^{2}} dx = \int_{- \infty}^{+ \infty} \frac{\sin (\frac{π}{2} - x)}{1 + x^{2}} dx

\Rightarrow f (x) = \int_{- \infty}^{\infty} \frac{cosx}{1 + x^{2}} dx \Rightarrow f (- x) = \int_{- \infty}^{\infty} \frac{cosx}{1 + x^{2}} dx

\Rightarrow f (x) = 2 \int_{0}^{\infty} \frac{cosx}{1 + x^{2}} dx

A n y i d e a t o p r o c e e d ?

Answered by Dwaipayan Shikari last updated on 06/Jul/20

\int_{- \infty}^{\infty} \frac{s i n (x + \frac{π}{2})}{1 + x^{2}} d x = \int_{- \infty}^{\infty} \frac{c o s x}{1 + {t a n}^{2} θ} {s e c}^{2} θ d θ {t a k e x a s t a n θ

\int_{- \frac{π}{2}}^{\frac{π}{2}} c o s (t a n θ) d θ \dots . c o n t i n u e

Answered by mathmax by abdo last updated on 06/Jul/20

sir rohit want real method \dots!

Commented by prakash jain last updated on 06/Jul/20

Yez . I had this vidro link saved so

i shared it anyway .