Question Number 58362 by peter frank last updated on 22/Apr/19
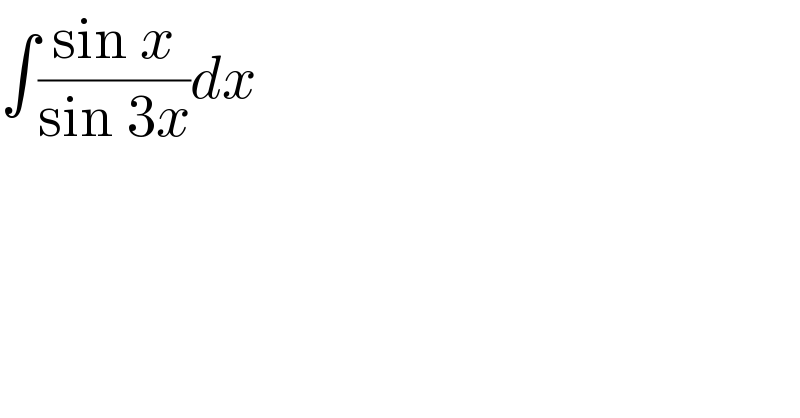
$$\int\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{3}{x}}{dx} \\ $$
Answered by mr W last updated on 22/Apr/19

$$=\int\frac{\mathrm{sin}\:{x}}{\mathrm{3}\:\mathrm{sin}\:{x}−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:{x}}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{3}−\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2cos}\:\mathrm{2}{x}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\mathrm{2}{x}}\:{d}\mathrm{2}{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\:\mid\frac{\mathrm{tan}\:\frac{{t}}{\mathrm{2}}+\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{{t}}{\mathrm{2}}−\sqrt{\mathrm{3}}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\:\mid\frac{\mathrm{tan}\:{x}+\sqrt{\mathrm{3}}}{\mathrm{tan}\:{x}−\sqrt{\mathrm{3}}}\mid+{C} \\ $$
Commented by peter frank last updated on 23/Apr/19

$${thanks} \\ $$
