Question Number 43346 by peter frank last updated on 10/Sep/18
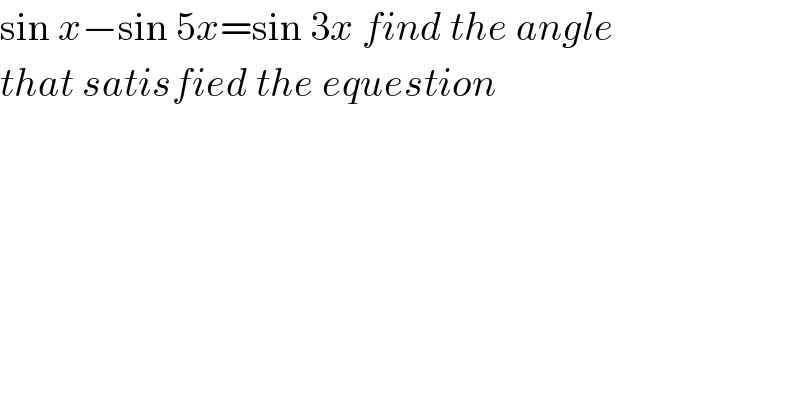
$$\mathrm{sin}\:{x}−\mathrm{sin}\:\mathrm{5}{x}=\mathrm{sin}\:\mathrm{3}{x}\:{find}\:{the}\:{angle} \\ $$$${that}\:{satisfied}\:{the}\:{equestion} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

$${sinx}={sin}\mathrm{5}{x}+{sin}\mathrm{3}{x} \\ $$$${sinx}=\mathrm{2}{sin}\mathrm{4}{x}.{cosx} \\ $$$${sinx}=\mathrm{2}\left(\mathrm{2}{sin}\mathrm{2}{xcos}\mathrm{2}{x}\right){cosx} \\ $$$${sinx}=\mathrm{4}\left(\mathrm{2}{sinxcosx}\right){cos}\mathrm{2}{xcosx} \\ $$$${sinx}−\mathrm{8}{sinxcos}^{\mathrm{2}} {x}.{cos}\mathrm{2}{x}=\mathrm{0} \\ $$$${sinx}\left(\mathrm{1}−\mathrm{8}{cos}^{\mathrm{2}} {x}.{cos}\mathrm{2}{x}\right)=\mathrm{0} \\ $$$${one}\:{solution} \\ $$$${sinx}=\mathrm{0}={sinn}\Pi \\ $$$${x}={n}\Pi \\ $$$$\mathrm{1}−\mathrm{8}{cos}^{\mathrm{2}} {x}.{cos}\mathrm{2}{x}=\mathrm{0} \\ $$$$\mathrm{4}\left(\mathrm{2}{cos}^{\mathrm{2}} {x}\right){cos}\mathrm{2}{x}=\mathrm{1} \\ $$$$\mathrm{4}\left(\mathrm{1}+{cos}\mathrm{2}{x}\right){cos}\mathrm{2}{x}=\mathrm{1} \\ $$$${a}={cos}\mathrm{2}{x} \\ $$$$\mathrm{4}\left(\mathrm{1}+{a}\right){a}=\mathrm{1} \\ $$$$\mathrm{4}{a}+\mathrm{4}{a}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{a}−\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}×\mathrm{4}×\left(−\mathrm{1}\right)}\:}{\mathrm{2}×\mathrm{4}} \\ $$$${a}=\frac{−\mathrm{4}\pm\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{2}×\mathrm{4}} \\ $$$${a}=\frac{\mathrm{4}\sqrt{\mathrm{2}}\:−\mathrm{4}}{\mathrm{2}×\mathrm{4}}\:\:{and}\:\frac{−\mathrm{4}\sqrt{\mathrm{2}}\:−\mathrm{4}}{\mathrm{2}×\mathrm{4}} \\ $$$${a}=\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{2}}\:\:{and}\:\frac{−\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}{\mathrm{2}}\leftarrow{this}\:{not}\:{feasible}\:{soln} \\ $$$$\:\:\:\:\mathrm{1}\geqslant{cos}\mathrm{2}{x}\geqslant−\mathrm{1}\: \\ $$$${so}\:{cos}\mathrm{2}{x}\:{can}\:{not}\:{be}\:\frac{−\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${cos}\mathrm{2}{x}=\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{2}}\approx{cos}\mathrm{78}^{{o}} \\ $$$${x}\approx\mathrm{39}^{{o}} \\ $$$${recheck} \\ $$$${sinx}−{sin}\mathrm{5}{x}={sin}\mathrm{3}{x} \\ $$$${LHS} \\ $$$${sin}\mathrm{39}^{{o}} −{sin}\left(\mathrm{195}^{{o}} \right) \\ $$$$\approx\mathrm{0}.\mathrm{89} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${RHS}\: \\ $$$${sin}\left(\mathrm{117}^{{o}} \right) \\ $$$$\approx\mathrm{0}.\mathrm{89} \\ $$$$ \\ $$
