sin-x-x-dx-

Question Number 102911 by I want to learn more last updated on 11/Jul/20

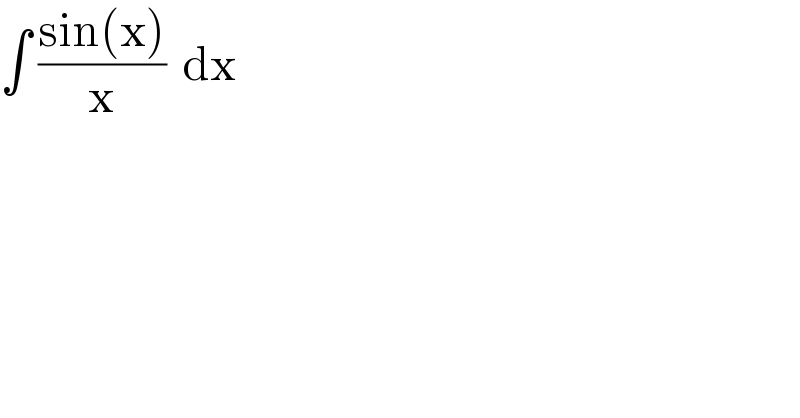
$$\int\:\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\:\:\mathrm{dx} \\ $$

Commented by prakash jain last updated on 11/Jul/20

This question has been asked so many times. Among most recent is Q98713

$$\mathrm{This}\:\mathrm{question}\:\mathrm{has}\:\mathrm{been}\:\mathrm{asked}\:\mathrm{so}\:\mathrm{many} \\ $$$$\mathrm{times}.\:\mathrm{Among}\:\mathrm{most}\:\mathrm{recent}\:\mathrm{is}\:\mathrm{Q98713} \\ $$

Answered by Dwaipayan Shikari last updated on 11/Jul/20

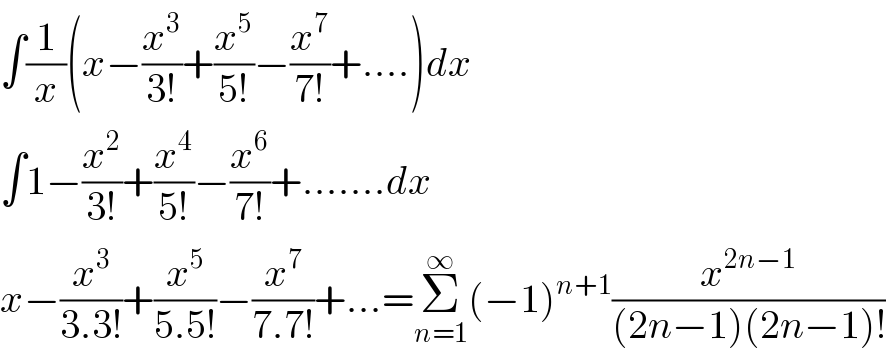
∫(1/x)(x−(x^3 /(3!))+(x^5 /(5!))−(x^7 /(7!))+....)dx ∫1−(x^2 /(3!))+(x^4 /(5!))−(x^6 /(7!))+.......dx x−(x^3 /(3.3!))+(x^5 /(5.5!))−(x^7 /(7.7!))+...=Σ_(n=1) ^∞ (−1)^(n+1) (x^(2n−1) /((2n−1)(2n−1)!))

$$\int\frac{\mathrm{1}}{{x}}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}!}+….\right){dx} \\ $$$$\int\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{5}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{7}!}+…….{dx} \\ $$$${x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}.\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}.\mathrm{5}!}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}.\mathrm{7}!}+…=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{{x}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$

Commented by I want to learn more last updated on 11/Jul/20