Question Number 182854 by manxsol last updated on 16/Dec/22
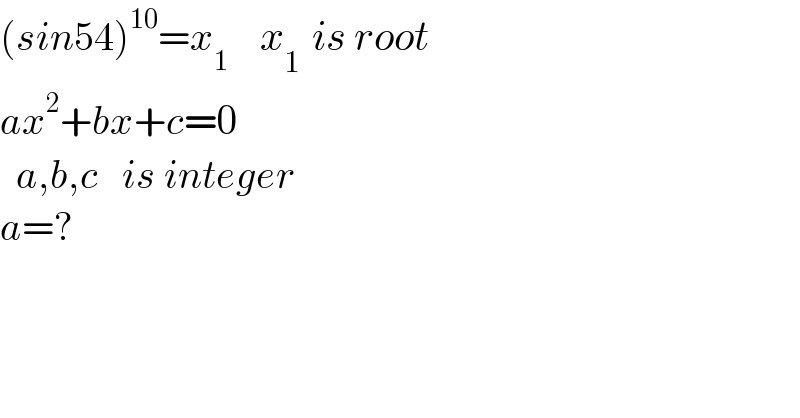
$$\left({sin}\mathrm{54}\right)^{\mathrm{10}} ={x}_{\mathrm{1}} \:\:\:\:{x}_{\mathrm{1}\:\:} {is}\:{root} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\:\:{a},{b},{c}\:\:\:{is}\:{integer} \\ $$$${a}=? \\ $$
Commented by manxsol last updated on 16/Dec/22
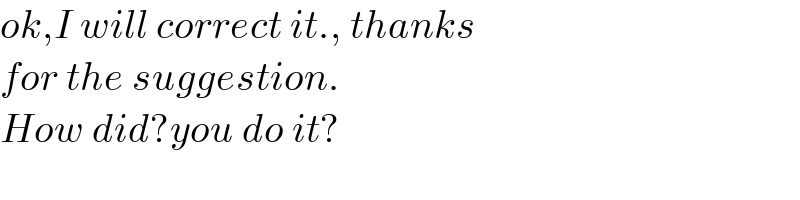
$${ok},{I}\:{will}\:{correct}\:{it}.,\:{thanks}\: \\ $$$${for}\:{the}\:{suggestion}. \\ $$$${How}\:{did}?{you}\:{do}\:{it}? \\ $$
Commented by Frix last updated on 15/Dec/22
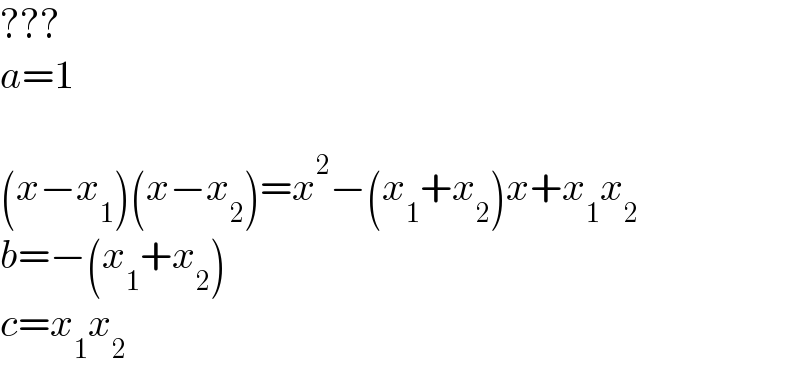
$$??? \\ $$$${a}=\mathrm{1} \\ $$$$ \\ $$$$\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)={x}^{\mathrm{2}} −\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right){x}+{x}_{\mathrm{1}} {x}_{\mathrm{2}} \\ $$$${b}=−\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right) \\ $$$${c}={x}_{\mathrm{1}} {x}_{\mathrm{2}} \\ $$
Commented by manxsol last updated on 15/Dec/22

$${sorry},\:{i}\:{am}\:{edit}\:{problem} \\ $$
Commented by manxsol last updated on 15/Dec/22

$${thanks} \\ $$
Commented by Frix last updated on 15/Dec/22
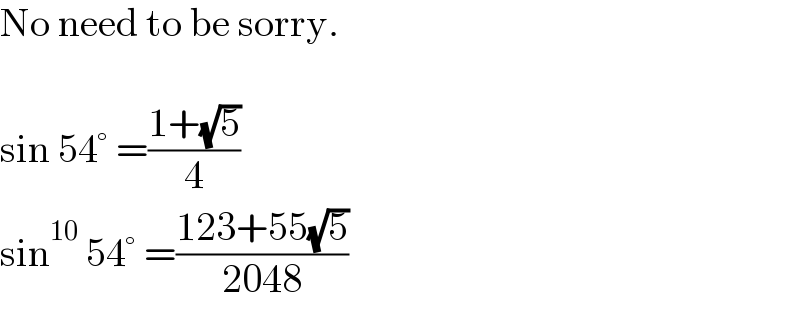
$$\mathrm{No}\:\mathrm{need}\:\mathrm{to}\:\mathrm{be}\:\mathrm{sorry}. \\ $$$$ \\ $$$$\mathrm{sin}\:\mathrm{54}°\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{10}} \:\mathrm{54}°\:=\frac{\mathrm{123}+\mathrm{55}\sqrt{\mathrm{5}}}{\mathrm{2048}} \\ $$
Commented by manxsol last updated on 15/Dec/22
![I solved it like this sin54=(((√5)+1)/4)=(1/2) (((√5)+1)/2)=(1/2)Φ ((1/2))^(10) Φ^(10) =(1/(1024)) (((123+55(√5))/2)) =((123+55(√5))/(2048))=x_1 See (★)^ roots integer⇒x_(2 conjugate) x_2 =((123−55(√5))/(2048)) x_1 +x_2 =((246)/(2048)) x_1 x_2 =(4/(4194304)) calculate using editor tinku tara 2048^2 4194304.0 123^2 −5×55^2 4.0 246×2048 503808.0 4194304/4 1048576.0 503808/4 125952.0 input 4×5 [push] enter [push] ⋮ [push] calcular 20.0 x^2 −((246)/(2048))x+(4/(4194304))=0 4194304x^2 −503808x+4=0 1048576x^2 −125952x+1=0 solution: a=1048576 (★) Φ^(10) =(((1+(√5))/2))^(10) =((123+55(√5))/2) serie de fibonacci determinant ((1,2,3,4,5,6,7,8,9,(10),(11)),(1,1,2,3,5,8,(13),(21),(34),(55),(89))) a=55 b=123 deduccion hecha de tabla de potencias de Φ=(1+(√5))/2](https://www.tinkutara.com/question/Q182871.png)
$$ \\ $$$${I}\:{solved}\:{it}\:{like}\:{this} \\ $$$${sin}\mathrm{54}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\Phi \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{10}} \Phi^{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{1024}}\:\left(\frac{\mathrm{123}+\mathrm{55}\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{123}+\mathrm{55}\sqrt{\mathrm{5}}}{\mathrm{2048}}={x}_{\mathrm{1}} \\ $$$${See}\:\left(\bigstar\right)^{} \\ $$$${roots}\:{integer}\Rightarrow{x}_{\mathrm{2}\:{conjugate}} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{123}−\mathrm{55}\sqrt{\mathrm{5}}}{\mathrm{2048}} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\frac{\mathrm{246}}{\mathrm{2048}} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{4194304}} \\ $$$${calculate}\:\:{using}\:{editor}\:{tinku}\:{tara} \\ $$$$\mathrm{2048}^{\mathrm{2}} \\ $$$$\mathrm{4194304}.\mathrm{0} \\ $$$$\mathrm{123}^{\mathrm{2}} −\mathrm{5}×\mathrm{55}^{\mathrm{2}} \\ $$$$\mathrm{4}.\mathrm{0} \\ $$$$\mathrm{246}×\mathrm{2048} \\ $$$$\mathrm{503808}.\mathrm{0} \\ $$$$\mathrm{4194304}/\mathrm{4} \\ $$$$\mathrm{1048576}.\mathrm{0} \\ $$$$\mathrm{503808}/\mathrm{4} \\ $$$$\mathrm{125952}.\mathrm{0} \\ $$$${input}\: \\ $$$$\mathrm{4}×\mathrm{5} \\ $$$$\left[{push}\right]\:\:\:{enter} \\ $$$$\left[{push}\right]\:\:\:\vdots \\ $$$$\left[{push}\right]\:\:\:{calcular} \\ $$$$\mathrm{20}.\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{246}}{\mathrm{2048}}{x}+\frac{\mathrm{4}}{\mathrm{4194304}}=\mathrm{0} \\ $$$$\mathrm{4194304}{x}^{\mathrm{2}} −\mathrm{503808}{x}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{1048576}{x}^{\mathrm{2}} −\mathrm{125952}{x}+\mathrm{1}=\mathrm{0} \\ $$$${solution}:\:\:{a}=\mathrm{1048576} \\ $$$$ \\ $$$$ \\ $$$$\left(\bigstar\right) \\ $$$$\Phi^{\mathrm{10}} =\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{10}} \:\:=\frac{\mathrm{123}+\mathrm{55}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${serie}\:{de}\:{fibonacci} \\ $$$$\begin{array}{|c|c|}{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{6}}&\hline{\mathrm{7}}&\hline{\mathrm{8}}&\hline{\mathrm{9}}&\hline{\mathrm{10}}&\hline{\mathrm{11}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{5}}&\hline{\mathrm{8}}&\hline{\mathrm{13}}&\hline{\mathrm{21}}&\hline{\mathrm{34}}&\hline{\mathrm{55}}&\hline{\mathrm{89}}\\\hline\end{array} \\ $$$$ \\ $$$${a}=\mathrm{55} \\ $$$${b}=\mathrm{123} \\ $$$${deduccion}\:{hecha}\:{de}\:{tabla}\:{de} \\ $$$${potencias}\:{de}\:\Phi=\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)/\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Frix last updated on 15/Dec/22
$$\mathrm{You}\:\mathrm{wrote}\:{a}\:{is}\:{integer}. \\ $$$$\mathrm{You}\:\mathrm{should}\:\mathrm{have}\:\mathrm{written}\:{a},\:{b},\:{c}\:\mathrm{are}\:\mathrm{integer}. \\ $$
