Menu Close

sin7-cos2-2-Find-

Tinku Tara 0 Comments
Pin




Question Number 99433 by Dwaipayan Shikari last updated on 20/Jun/20
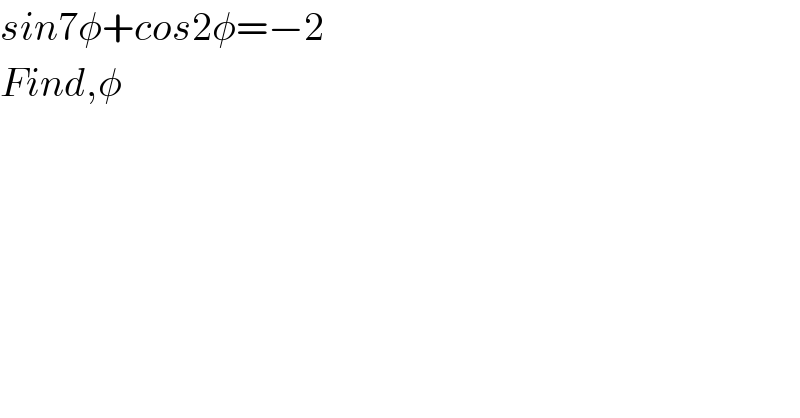
sin7φ+cos2φ=−2 Find,φ
$${sin}\mathrm{7}\phi+{cos}\mathrm{2}\phi=−\mathrm{2} \\ $$$${Find},\phi \\ $$
Commented by bobhans last updated on 21/Jun/20
sin 7∅+sin (90−2∅)=−2 2sin (((90+5∅)/2)) cos (((9∅−90)/2)) = −2 sin (((90+5∅)/2)) cos (((9∅−90)/2)) = −1 case (1) { ((sin (((90+5∅)/2)) = −1)),((cos (((9∅−90)/2)) = 1)) :} case(2) { ((sin (((90+5∅)/2)) = 1)),((cos (((9∅−90)/2)) = −1)) :}
$$\mathrm{sin}\:\mathrm{7}\emptyset+\mathrm{sin}\:\left(\mathrm{90}−\mathrm{2}\emptyset\right)=−\mathrm{2} \\ $$$$\mathrm{2sin}\:\left(\frac{\mathrm{90}+\mathrm{5}\emptyset}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{\mathrm{9}\emptyset−\mathrm{90}}{\mathrm{2}}\right)\:=\:−\mathrm{2} \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{90}+\mathrm{5}\emptyset}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{\mathrm{9}\emptyset−\mathrm{90}}{\mathrm{2}}\right)\:=\:−\mathrm{1} \\ $$$$\mathrm{case}\:\left(\mathrm{1}\right)\: \\ $$$$\begin{cases}{\mathrm{sin}\:\left(\frac{\mathrm{90}+\mathrm{5}\emptyset}{\mathrm{2}}\right)\:=\:−\mathrm{1}}\\{\mathrm{cos}\:\left(\frac{\mathrm{9}\emptyset−\mathrm{90}}{\mathrm{2}}\right)\:=\:\mathrm{1}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{2}\right) \\ $$$$\begin{cases}{\mathrm{sin}\:\left(\frac{\mathrm{90}+\mathrm{5}\emptyset}{\mathrm{2}}\right)\:=\:\mathrm{1}}\\{\mathrm{cos}\:\left(\frac{\mathrm{9}\emptyset−\mathrm{90}}{\mathrm{2}}\right)\:=\:−\mathrm{1}}\end{cases} \\ $$
Answered by mr W last updated on 21/Jun/20
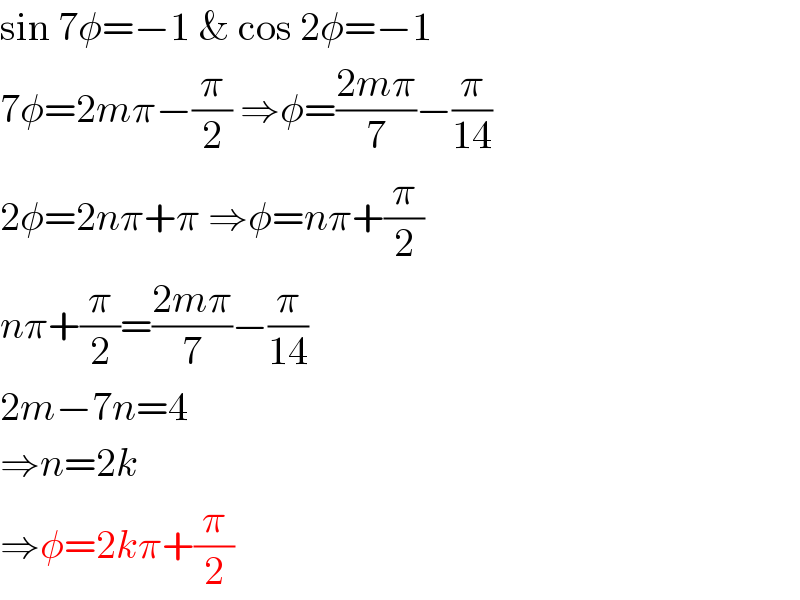
sin 7φ=−1 & cos 2φ=−1 7φ=2mπ−(π/2) ⇒φ=((2mπ)/7)−(π/(14)) 2φ=2nπ+π ⇒φ=nπ+(π/2) nπ+(π/2)=((2mπ)/7)−(π/(14)) 2m−7n=4 ⇒n=2k ⇒φ=2kπ+(π/2)
$$\mathrm{sin}\:\mathrm{7}\phi=−\mathrm{1}\:\&\:\mathrm{cos}\:\mathrm{2}\phi=−\mathrm{1} \\ $$$$\mathrm{7}\phi=\mathrm{2}{m}\pi−\frac{\pi}{\mathrm{2}}\:\Rightarrow\phi=\frac{\mathrm{2}{m}\pi}{\mathrm{7}}−\frac{\pi}{\mathrm{14}} \\ $$$$\mathrm{2}\phi=\mathrm{2}{n}\pi+\pi\:\Rightarrow\phi={n}\pi+\frac{\pi}{\mathrm{2}} \\ $$$${n}\pi+\frac{\pi}{\mathrm{2}}=\frac{\mathrm{2}{m}\pi}{\mathrm{7}}−\frac{\pi}{\mathrm{14}} \\ $$$$\mathrm{2}{m}−\mathrm{7}{n}=\mathrm{4} \\ $$$$\Rightarrow{n}=\mathrm{2}{k} \\ $$$$\Rightarrow\phi=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 21/Jun/20
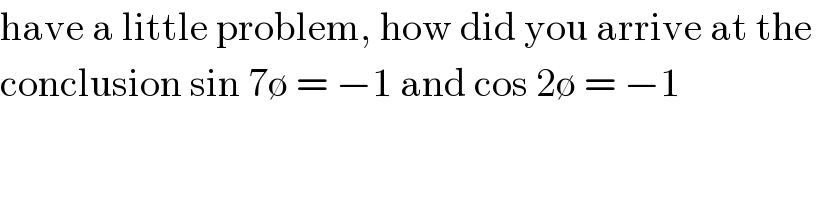
have a little problem, how did you arrive at the conclusion sin 7∅ = −1 and cos 2∅ = −1
$$\mathrm{have}\:\mathrm{a}\:\mathrm{little}\:\mathrm{problem},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{arrive}\:\mathrm{at}\:\mathrm{the}\: \\ $$$$\mathrm{conclusion}\:\mathrm{sin}\:\mathrm{7}\emptyset\:=\:−\mathrm{1}\:\mathrm{and}\:\mathrm{cos}\:\mathrm{2}\emptyset\:=\:−\mathrm{1} \\ $$
Commented by ChristopherPeter last updated on 21/Jun/20
jjn
Commented by floor(10²Eta[1]) last updated on 21/Jun/20
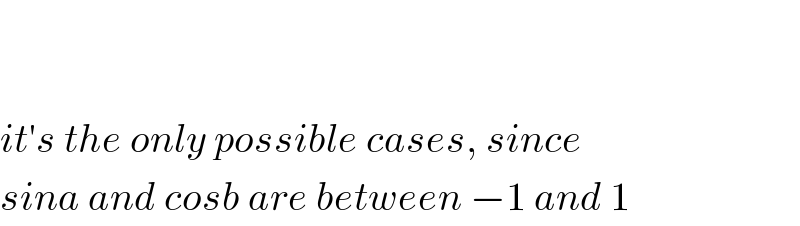
it′s the only possible cases, since sina and cosb are between −1 and 1
$$ \\ $$$$ \\ $$$${it}'{s}\:{the}\:{only}\:{possible}\:{cases},\:{since} \\ $$$${sina}\:{and}\:{cosb}\:{are}\:{between}\:−\mathrm{1}\:{and}\:\mathrm{1} \\ $$
Commented by mr W last updated on 21/Jun/20
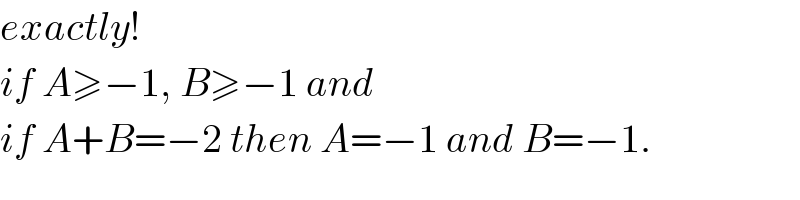
exactly! if A≥−1, B≥−1 and if A+B=−2 then A=−1 and B=−1.
$${exactly}! \\ $$$${if}\:{A}\geqslant−\mathrm{1},\:{B}\geqslant−\mathrm{1}\:{and} \\ $$$${if}\:{A}+{B}=−\mathrm{2}\:{then}\:{A}=−\mathrm{1}\:{and}\:{B}=−\mathrm{1}. \\ $$
Commented by 1549442205 last updated on 21/Jun/20
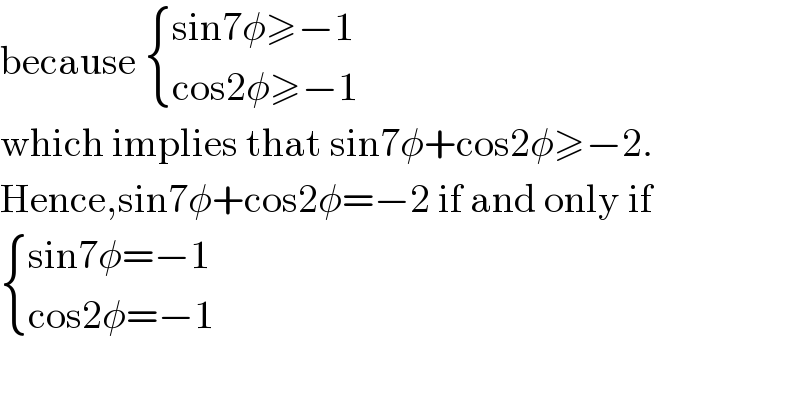
because { ((sin7φ≥−1)),((cos2φ≥−1)) :} which implies that sin7φ+cos2φ≥−2. Hence,sin7φ+cos2φ=−2 if and only if { ((sin7φ=−1)),((cos2φ=−1)) :}
$$\mathrm{because}\:\begin{cases}{\mathrm{sin7}\phi\geqslant−\mathrm{1}}\\{\mathrm{cos2}\phi\geqslant−\mathrm{1}}\end{cases}\: \\ $$$$\mathrm{which}\:\mathrm{implies}\:\mathrm{that}\:\mathrm{sin7}\phi+\mathrm{cos2}\phi\geqslant−\mathrm{2}. \\ $$$$\mathrm{Hence},\mathrm{sin7}\phi+\mathrm{cos2}\phi=−\mathrm{2}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\begin{cases}{\mathrm{sin7}\phi=−\mathrm{1}}\\{\mathrm{cos2}\phi=−\mathrm{1}}\end{cases} \\ $$$$ \\ $$
Answered by 1549442205 last updated on 21/Jun/20
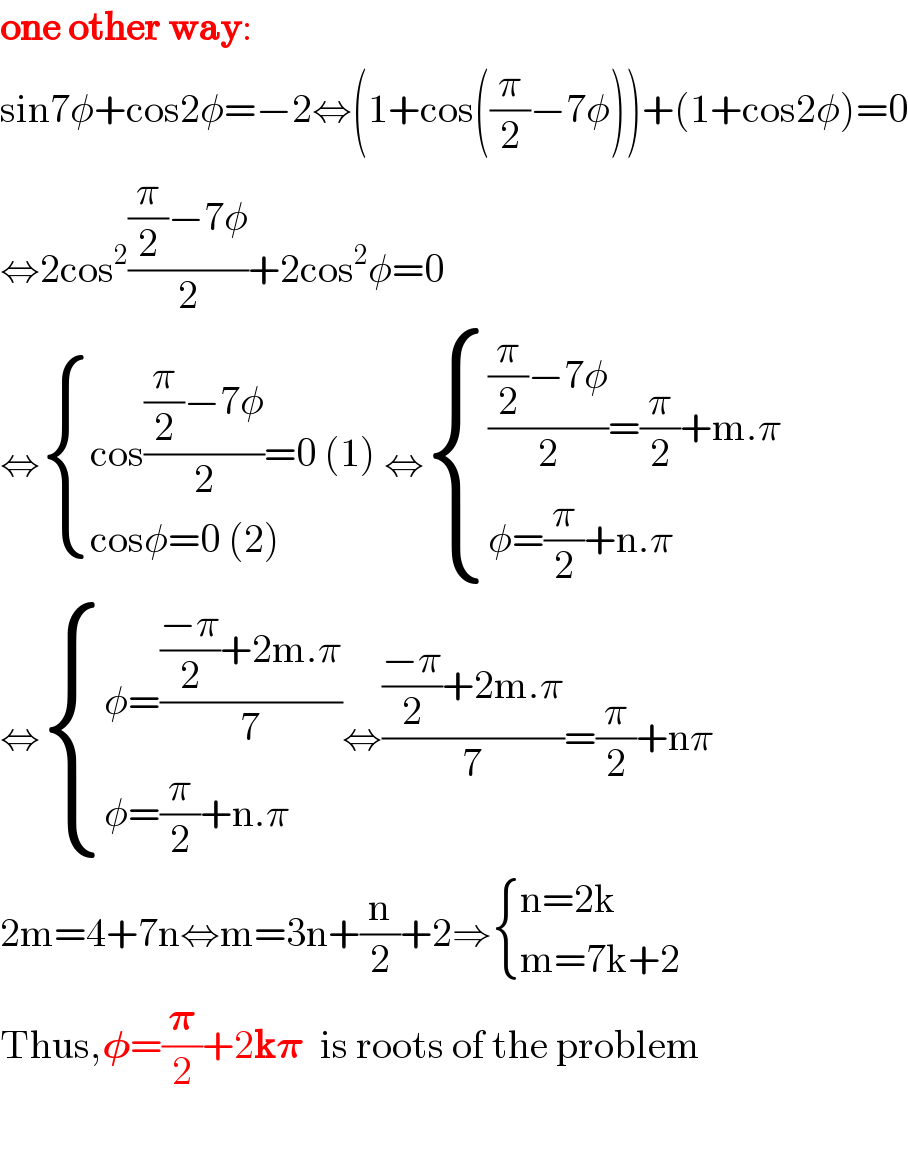
one other way: sin7φ+cos2φ=−2⇔(1+cos((π/2)−7φ))+(1+cos2φ)=0 ⇔2cos^2 (((π/2)−7φ)/2)+2cos^2 φ=0 ⇔ { ((cos(((π/2)−7φ)/2)=0 (1) )),((cosφ=0 (2))) :}⇔ { (((((π/2)−7φ)/2)=(π/2)+m.π)),((φ=(π/2)+n.π)) :} ⇔ { ((φ=((((−π)/2)+2m.π)/7))),((φ=(π/2)+n.π)) :}⇔((((−π)/2)+2m.π)/7)=(π/2)+nπ 2m=4+7n⇔m=3n+(n/2)+2⇒ { ((n=2k)),((m=7k+2)) :} Thus,𝛗=(𝛑/2)+2k𝛑 is roots of the problem
$$\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{other}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\mathrm{sin7}\phi+\mathrm{cos2}\phi=−\mathrm{2}\Leftrightarrow\left(\mathrm{1}+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{7}\phi\right)\right)+\left(\mathrm{1}+\mathrm{cos2}\phi\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2cos}^{\mathrm{2}} \frac{\frac{\pi}{\mathrm{2}}−\mathrm{7}\phi}{\mathrm{2}}+\mathrm{2cos}^{\mathrm{2}} \phi=\mathrm{0} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{cos}\frac{\frac{\pi}{\mathrm{2}}−\mathrm{7}\phi}{\mathrm{2}}=\mathrm{0}\:\left(\mathrm{1}\right)\:}\\{\mathrm{cos}\phi=\mathrm{0}\:\left(\mathrm{2}\right)}\end{cases}\Leftrightarrow\begin{cases}{\frac{\frac{\pi}{\mathrm{2}}−\mathrm{7}\phi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}+\mathrm{m}.\pi}\\{\phi=\frac{\pi}{\mathrm{2}}+\mathrm{n}.\pi}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\phi=\frac{\frac{−\pi}{\mathrm{2}}+\mathrm{2m}.\pi}{\mathrm{7}}}\\{\phi=\frac{\pi}{\mathrm{2}}+\mathrm{n}.\pi}\end{cases}\Leftrightarrow\frac{\frac{−\pi}{\mathrm{2}}+\mathrm{2m}.\pi}{\mathrm{7}}=\frac{\pi}{\mathrm{2}}+\mathrm{n}\pi \\ $$$$\mathrm{2m}=\mathrm{4}+\mathrm{7n}\Leftrightarrow\mathrm{m}=\mathrm{3n}+\frac{\mathrm{n}}{\mathrm{2}}+\mathrm{2}\Rightarrow\begin{cases}{\mathrm{n}=\mathrm{2k}}\\{\mathrm{m}=\mathrm{7k}+\mathrm{2}}\end{cases} \\ $$$$\mathrm{Thus},\boldsymbol{\phi}=\frac{\boldsymbol{\pi}}{\mathrm{2}}+\mathrm{2}\boldsymbol{\mathrm{k}\pi}\:\:\mathrm{is}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{problem} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *