Question Number 150661 by Jamshidbek last updated on 14/Aug/21
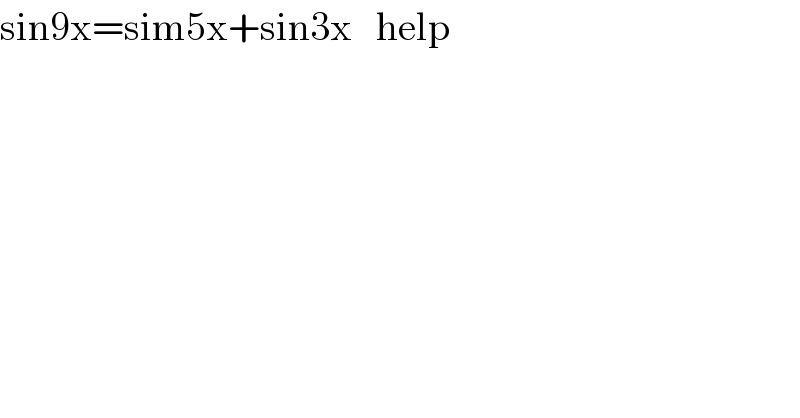
$$\mathrm{sin9x}=\mathrm{sim5x}+\mathrm{sin3x}\:\:\:\mathrm{help}\: \\ $$
Commented by MJS_new last updated on 15/Aug/21
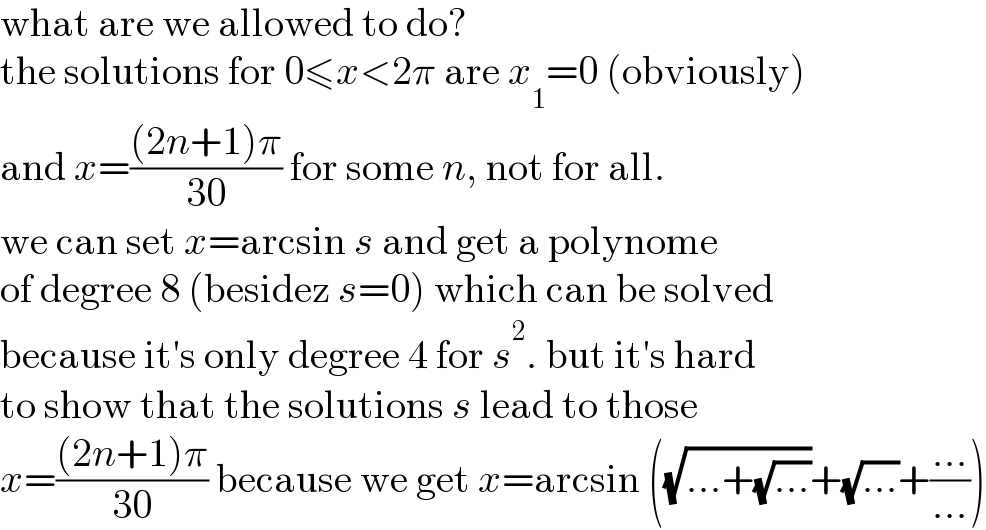
$$\mathrm{what}\:\mathrm{are}\:\mathrm{we}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{do}? \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:\mathrm{are}\:{x}_{\mathrm{1}} =\mathrm{0}\:\left(\mathrm{obviously}\right) \\ $$$$\mathrm{and}\:{x}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{30}}\:\mathrm{for}\:\mathrm{some}\:{n},\:\mathrm{not}\:\mathrm{for}\:\mathrm{all}. \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{set}\:{x}=\mathrm{arcsin}\:{s}\:\mathrm{and}\:\mathrm{get}\:\mathrm{a}\:\mathrm{polynome} \\ $$$$\mathrm{of}\:\mathrm{degree}\:\mathrm{8}\:\left(\mathrm{besidez}\:{s}=\mathrm{0}\right)\:\mathrm{which}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$$$\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{degree}\:\mathrm{4}\:\mathrm{for}\:{s}^{\mathrm{2}} .\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{hard} \\ $$$$\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{solutions}\:{s}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{those} \\ $$$${x}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{30}}\:\mathrm{because}\:\mathrm{we}\:\mathrm{get}\:{x}=\mathrm{arcsin}\:\left(\sqrt{…+\sqrt{…}}+\sqrt{…}+\frac{…}{…}\right) \\ $$
