Question Number 123694 by Dwaipayan Shikari last updated on 27/Nov/20
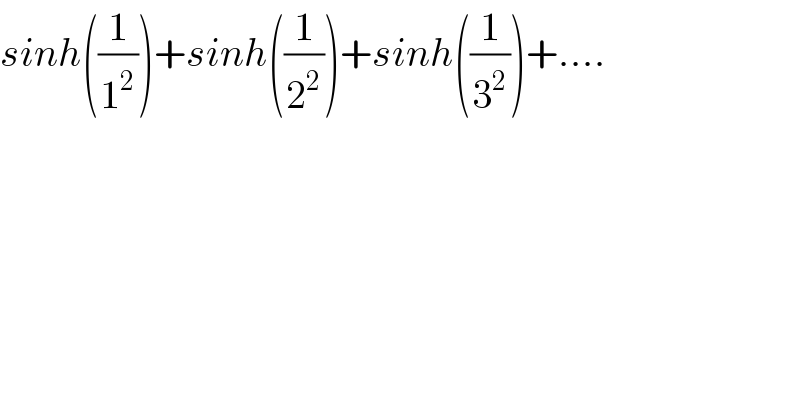
$${sinh}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }\right)+{sinh}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)+{sinh}\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)+…. \\ $$
Commented by Dwaipayan Shikari last updated on 27/Nov/20

$${Another}\:{approximation}\:{of}\:{sin}\left(\frac{\pi}{\mathrm{9}}\right) \\ $$$${sin}\left(\frac{\pi}{\mathrm{9}}\right)=\frac{\pi}{\mathrm{9}}\overset{\infty} {\prod}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{81}{n}^{\mathrm{2}} }\right) \\ $$$${sin}\left(\frac{\pi}{\mathrm{9}}\right)=\frac{\pi}{\mathrm{9}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{27}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{36}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{45}^{\mathrm{2}} }\right)…. \\ $$
