Question Number 123460 by Dwaipayan Shikari last updated on 25/Nov/20
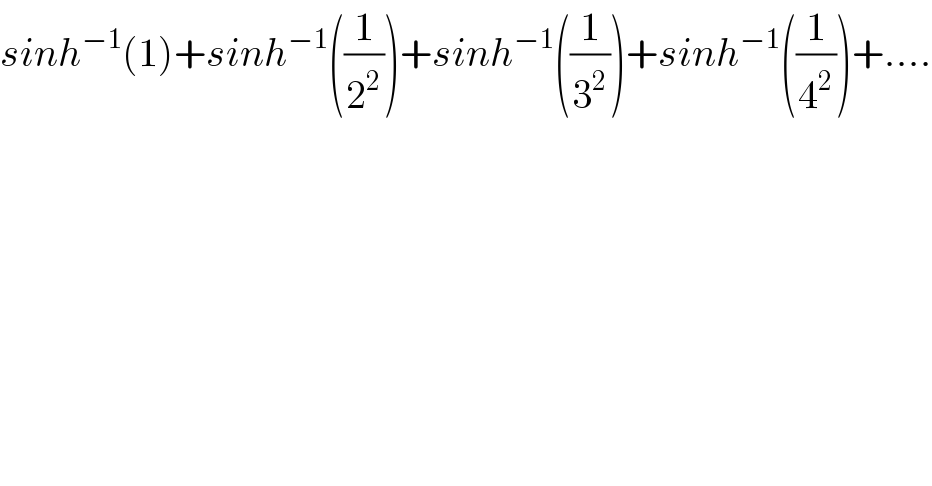
$${sinh}^{−\mathrm{1}} \left(\mathrm{1}\right)+{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)+{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)+{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\right)+…. \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 25/Nov/20
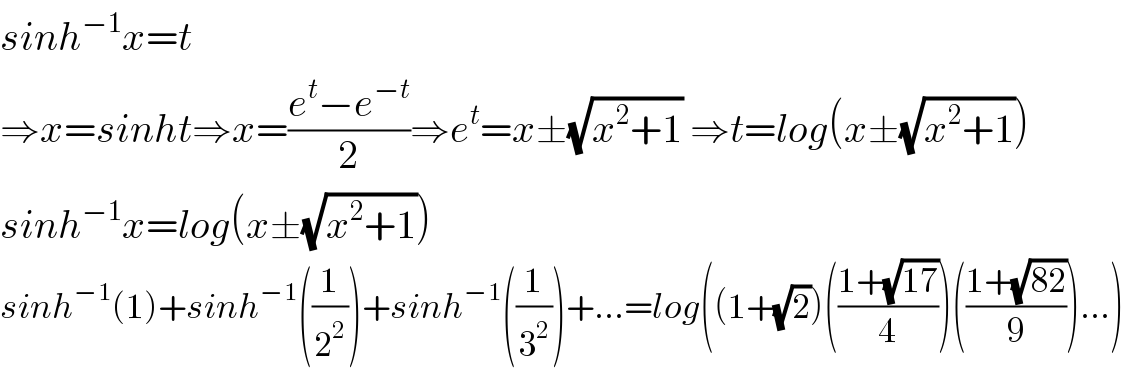
$${sinh}^{−\mathrm{1}} {x}={t} \\ $$$$\Rightarrow{x}={sinht}\Rightarrow{x}=\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\Rightarrow{e}^{{t}} ={x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow{t}={log}\left({x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${sinh}^{−\mathrm{1}} {x}={log}\left({x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${sinh}^{−\mathrm{1}} \left(\mathrm{1}\right)+{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)+{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\right)+…={log}\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left(\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{4}}\right)\left(\frac{\mathrm{1}+\sqrt{\mathrm{82}}}{\mathrm{9}}\right)…\right) \\ $$
