Question Number 90024 by Rio Michael last updated on 20/Apr/20
![sinh^(−1) [ln(x + (√(x^2 + 1)) )] = ?](https://www.tinkutara.com/question/Q90024.png)
$$\mathrm{sinh}^{−\mathrm{1}} \left[\mathrm{ln}\left({x}\:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:\right)\right]\:=\:? \\ $$
Commented by Rio Michael last updated on 21/Apr/20

$$\mathrm{really}\:\mathrm{sir}, \\ $$$$\mathrm{how}\:\mathrm{about}\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{sinh}\left(\mathrm{ln}\:\left({x}\:+\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\right)\:\right. \\ $$
Commented by MJS last updated on 21/Apr/20
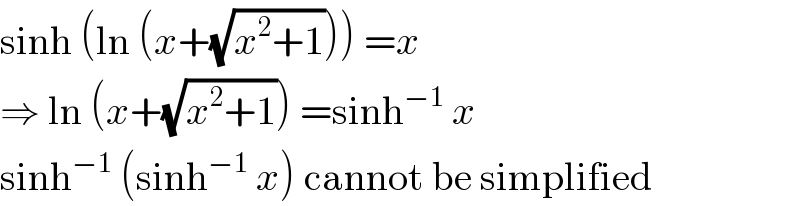
$$\mathrm{sinh}\:\left(\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\right)\:={x} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\:=\mathrm{sinh}^{−\mathrm{1}} \:{x} \\ $$$$\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{sinh}^{−\mathrm{1}} \:{x}\right)\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{simplified} \\ $$
