Question Number 102298 by Ar Brandon last updated on 08/Jul/20
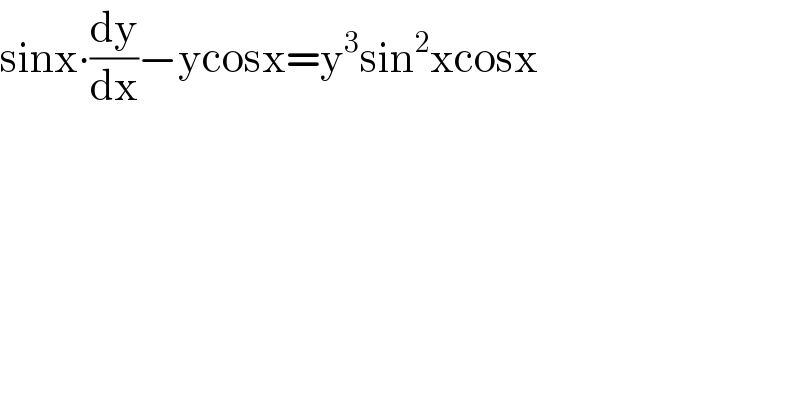
$$\mathrm{sinx}\centerdot\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{ycosx}=\mathrm{y}^{\mathrm{3}} \mathrm{sin}^{\mathrm{2}} \mathrm{xcosx} \\ $$
Answered by john santu last updated on 08/Jul/20
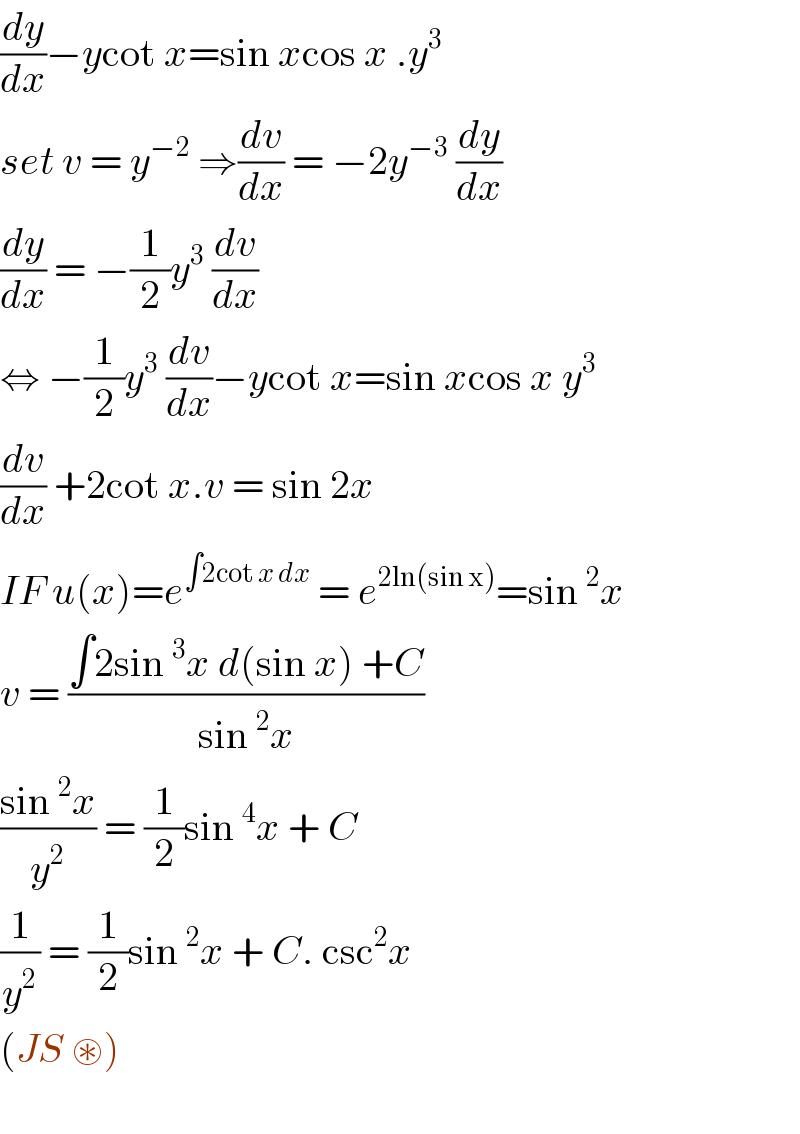
$$\frac{{dy}}{{dx}}−{y}\mathrm{cot}\:{x}=\mathrm{sin}\:{x}\mathrm{cos}\:{x}\:.{y}^{\mathrm{3}} \\ $$$${set}\:{v}\:=\:{y}^{−\mathrm{2}} \:\Rightarrow\frac{{dv}}{{dx}}\:=\:−\mathrm{2}{y}^{−\mathrm{3}} \:\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{3}} \:\frac{{dv}}{{dx}} \\ $$$$\Leftrightarrow\:−\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{3}} \:\frac{{dv}}{{dx}}−{y}\mathrm{cot}\:{x}=\mathrm{sin}\:{x}\mathrm{cos}\:{x}\:{y}^{\mathrm{3}} \\ $$$$\frac{{dv}}{{dx}}\:+\mathrm{2cot}\:{x}.{v}\:=\:\mathrm{sin}\:\mathrm{2}{x} \\ $$$${IF}\:{u}\left({x}\right)={e}^{\int\mathrm{2cot}\:{x}\:{dx}} \:=\:{e}^{\mathrm{2ln}\left(\mathrm{sin}\:\mathrm{x}\right)} =\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$${v}\:=\:\frac{\int\mathrm{2sin}\:^{\mathrm{3}} {x}\:{d}\left(\mathrm{sin}\:{x}\right)\:+{C}}{\mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$$\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{{y}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{4}} {x}\:+\:{C}\: \\ $$$$\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} {x}\:+\:{C}.\:\mathrm{csc}^{\mathrm{2}} {x}\: \\ $$$$\left({JS}\:\circledast\right) \\ $$$$ \\ $$
