Question Number 163072 by abdullahhhhh last updated on 03/Jan/22

$$\int\frac{\boldsymbol{\mathrm{sinx}}+\boldsymbol{\mathrm{sin}}\mathrm{3}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{sin}}\mathrm{5}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{sin}}\mathrm{7}\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{cosx}}+\boldsymbol{\mathrm{cos}}\mathrm{3}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}\mathrm{5}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}\mathrm{7}\boldsymbol{\mathrm{x}}}\:\boldsymbol{\mathrm{dx}} \\ $$
Answered by tounghoungko last updated on 03/Jan/22
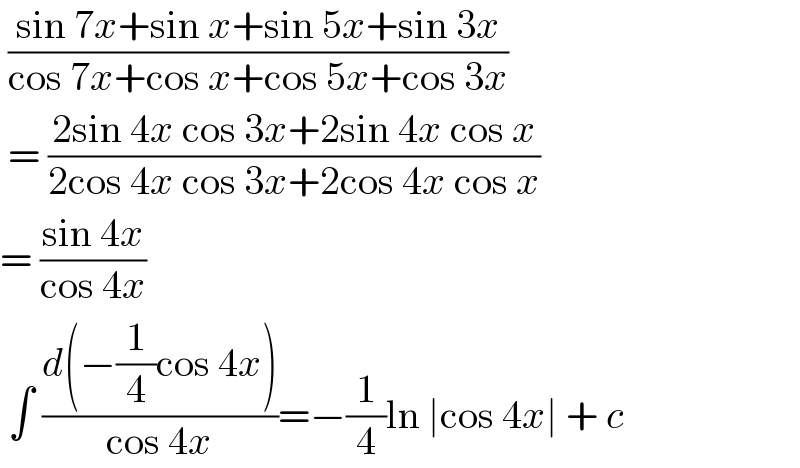
$$\:\frac{\mathrm{sin}\:\mathrm{7}{x}+\mathrm{sin}\:{x}+\mathrm{sin}\:\mathrm{5}{x}+\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{cos}\:\mathrm{7}{x}+\mathrm{cos}\:{x}+\mathrm{cos}\:\mathrm{5}{x}+\mathrm{cos}\:\mathrm{3}{x}}\: \\ $$$$\:=\:\frac{\mathrm{2sin}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{3}{x}+\mathrm{2sin}\:\mathrm{4}{x}\:\mathrm{cos}\:{x}}{\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{3}{x}+\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:{x}} \\ $$$$=\:\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{cos}\:\mathrm{4}{x}} \\ $$$$\:\int\:\frac{{d}\left(−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4}{x}\right)}{\mathrm{cos}\:\mathrm{4}{x}}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{4}{x}\mid\:+\:{c}\: \\ $$
Commented by tounghoungko last updated on 03/Jan/22
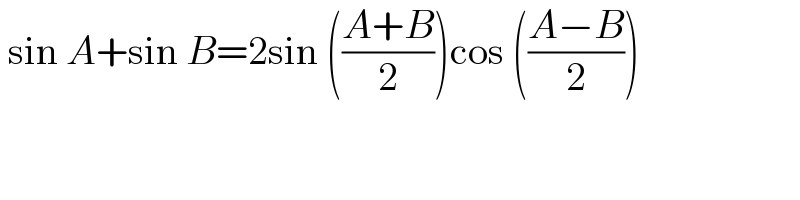
$$\:\mathrm{sin}\:{A}+\mathrm{sin}\:{B}=\mathrm{2sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right) \\ $$
Commented by Ar Brandon last updated on 03/Jan/22
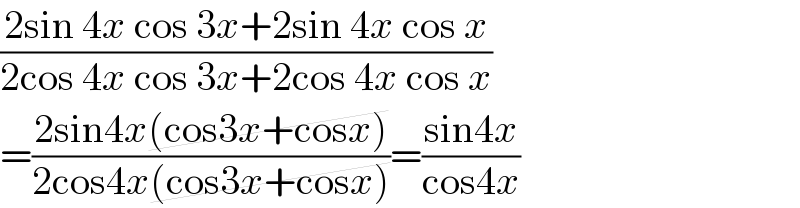
$$\frac{\mathrm{2sin}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{3}{x}+\mathrm{2sin}\:\mathrm{4}{x}\:\mathrm{cos}\:{x}}{\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{3}{x}+\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:{x}} \\ $$$$=\frac{\mathrm{2sin4}{x}\cancel{\left(\mathrm{cos3}{x}+\mathrm{cos}{x}\right)}}{\mathrm{2cos4}{x}\cancel{\left(\mathrm{cos3}{x}+\mathrm{cos}{x}\right)}}=\frac{\mathrm{sin4}{x}}{\mathrm{cos4}{x}} \\ $$
