Question Number 165995 by mathlove last updated on 11/Feb/22

$$\begin{cases}{{sinx}+{siny}=\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{2}^{\mathrm{sin}\:{x}} +\mathrm{2}^{\mathrm{sin}\:{y}} =\mathrm{2}+\sqrt{\mathrm{2}}}\end{cases}\:\:\:\:\:\:\:{faind}\:\:\:{x}=? \\ $$
Answered by alephzero last updated on 11/Feb/22
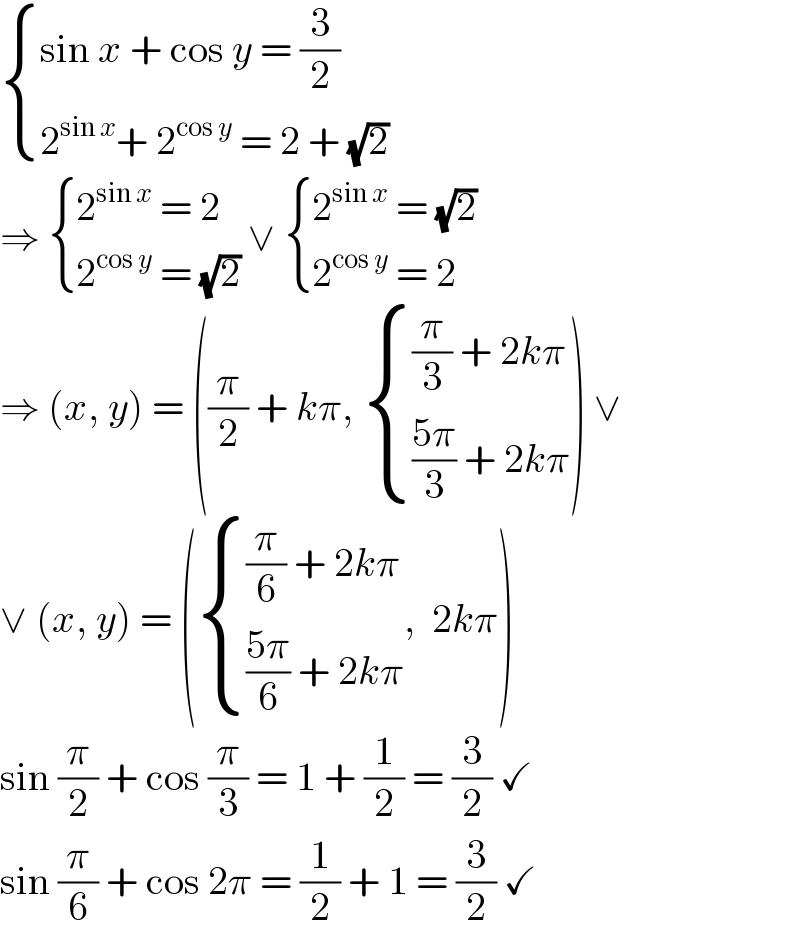
$$\begin{cases}{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{y}\:=\:\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{2}^{\mathrm{sin}\:{x}} +\:\mathrm{2}^{\mathrm{cos}\:{y}} \:=\:\mathrm{2}\:+\:\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{2}^{\mathrm{sin}\:{x}} \:=\:\mathrm{2}}\\{\mathrm{2}^{\mathrm{cos}\:{y}} \:=\:\sqrt{\mathrm{2}}}\end{cases}\:\vee\:\begin{cases}{\mathrm{2}^{\mathrm{sin}\:{x}} \:=\:\sqrt{\mathrm{2}}}\\{\mathrm{2}^{\mathrm{cos}\:{y}} \:=\:\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:\left({x},\:{y}\right)\:=\:\left(\frac{\pi}{\mathrm{2}}\:+\:{k}\pi,\:\begin{cases}{\frac{\pi}{\mathrm{3}}\:+\:\mathrm{2}{k}\pi}\\{\frac{\mathrm{5}\pi}{\mathrm{3}}\:+\:\mathrm{2}{k}\pi}\end{cases}\right)\:\vee \\ $$$$\vee\:\left({x},\:{y}\right)\:=\:\left(\begin{cases}{\frac{\pi}{\mathrm{6}}\:+\:\mathrm{2}{k}\pi}\\{\frac{\mathrm{5}\pi}{\mathrm{6}}\:+\:\mathrm{2}{k}\pi}\end{cases},\:\:\mathrm{2}{k}\pi\right) \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\:+\:\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:=\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\checkmark \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\:+\:\mathrm{cos}\:\mathrm{2}\pi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{1}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\checkmark \\ $$
