Question Number 174770 by Mastermind last updated on 10/Aug/22

$$\int\left(\frac{\mathrm{sinx}}{\:\sqrt{\mathrm{x}}}\right)\mathrm{dx} \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$
Answered by Frix last updated on 10/Aug/22
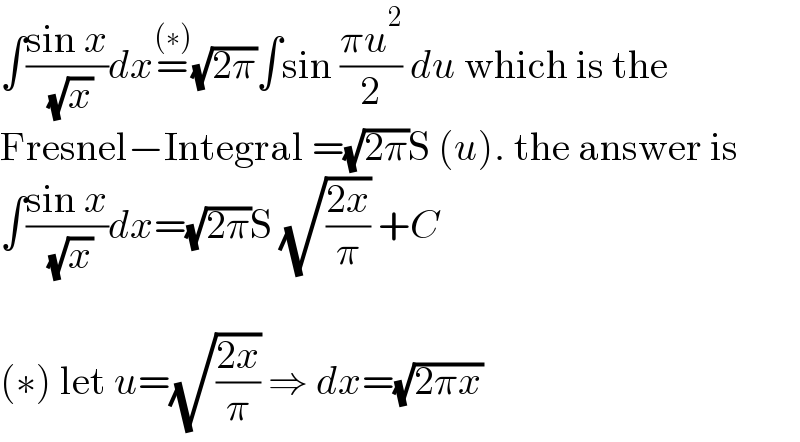
$$\int\frac{\mathrm{sin}\:{x}}{\:\sqrt{{x}}}{dx}\overset{\left(\ast\right)} {=}\sqrt{\mathrm{2}\pi}\int\mathrm{sin}\:\frac{\pi{u}^{\mathrm{2}} }{\mathrm{2}}\:{du}\:\mathrm{which}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{Fresnel}−\mathrm{Integral}\:=\sqrt{\mathrm{2}\pi}\mathrm{S}\:\left({u}\right).\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is} \\ $$$$\int\frac{\mathrm{sin}\:{x}}{\:\sqrt{{x}}}{dx}=\sqrt{\mathrm{2}\pi}\mathrm{S}\:\sqrt{\frac{\mathrm{2}{x}}{\pi}}\:+{C} \\ $$$$ \\ $$$$\left(\ast\right)\:\mathrm{let}\:{u}=\sqrt{\frac{\mathrm{2}{x}}{\pi}}\:\Rightarrow\:{dx}=\sqrt{\mathrm{2}\pi{x}} \\ $$
