Menu Close

sir-Ma-h-t-que-you-have-posted-dx-x-1-x-n-2-can-you-reposted-it-please-

Tinku Tara 0 Comments
Pin




Question Number 87692 by mind is power last updated on 05/Apr/20
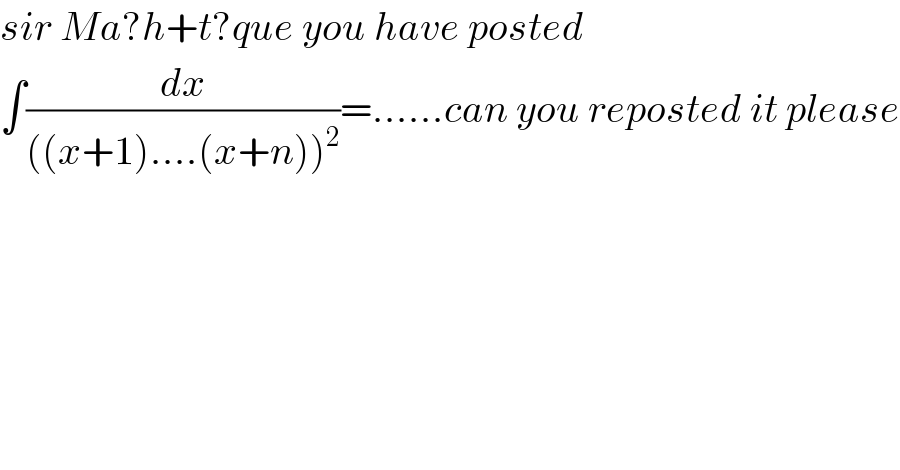
sir Ma?h+t?que you have posted ∫(dx/(((x+1)....(x+n))^2 ))=......can you reposted it please
$${sir}\:{Ma}?{h}+{t}?{que}\:{you}\:{have}\:{posted} \\ $$$$\int\frac{{dx}}{\left(\left({x}+\mathrm{1}\right)….\left({x}+{n}\right)\right)^{\mathrm{2}} }=……{can}\:{you}\:{reposted}\:{it}\:{please} \\ $$
Commented by M±th+et£s last updated on 05/Apr/20
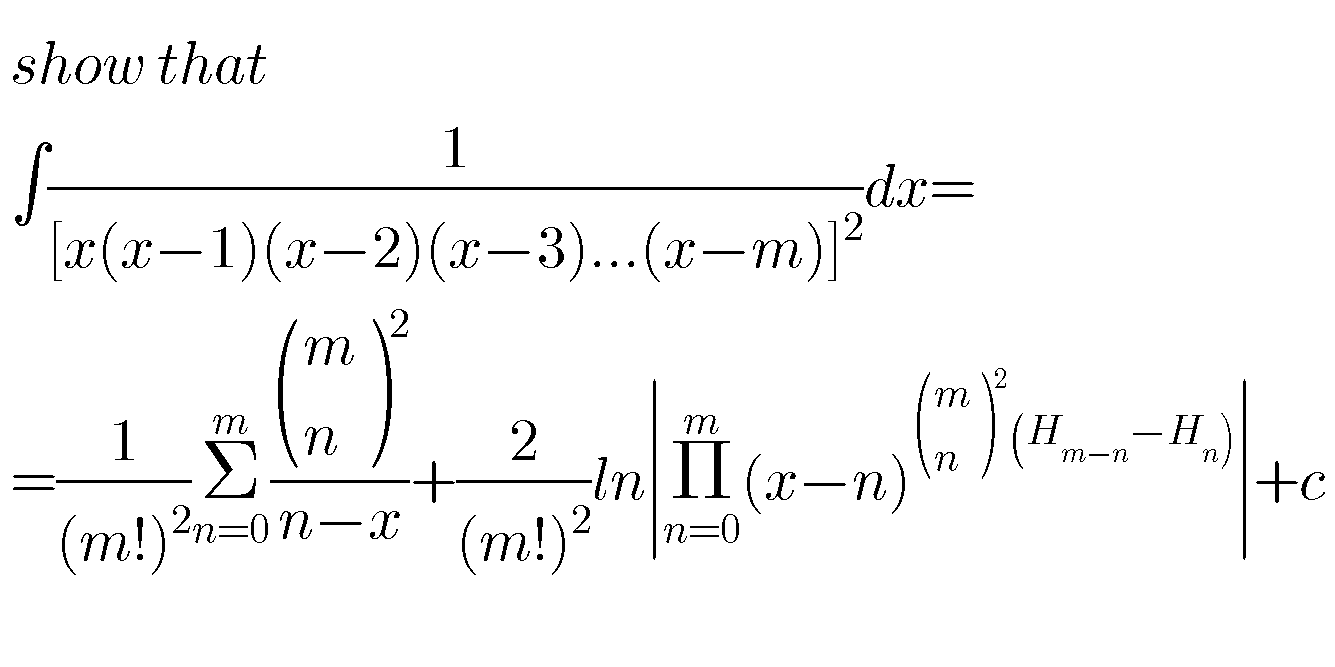
Commented by M±th+et£s last updated on 05/Apr/20
you meaen this sir
$${you}\:{meaen}\:{this}\:{sir} \\ $$
Commented by mind is power last updated on 05/Apr/20
yeah thanx
$${yeah}\:{thanx} \\ $$
Commented by M±th+et£s last updated on 05/Apr/20
you are welcome sir . hope you find a solution
$${you}\:{are}\:{welcome}\:{sir}\:.\:{hope}\:{you}\:{find}\:{a}\:{solution} \\ $$
Commented by mind is power last updated on 05/Apr/20
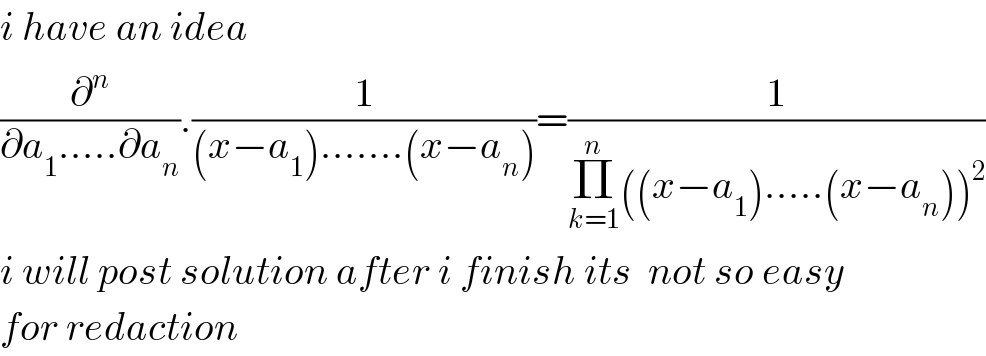
i have an idea (∂^n /(∂a_1 .....∂a_n )).(1/((x−a_1 ).......(x−a_n )))=(1/(Π_(k=1) ^n ((x−a_1 ).....(x−a_n ))^2 )) i will post solution after i finish its not so easy for redaction
$${i}\:{have}\:{an}\:{idea} \\ $$$$\frac{\partial^{{n}} }{\partial{a}_{\mathrm{1}} …..\partial{a}_{{n}} }.\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{1}} \right)…….\left({x}−{a}_{{n}} \right)}=\frac{\mathrm{1}}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\left({x}−{a}_{\mathrm{1}} \right)…..\left({x}−{a}_{{n}} \right)\right)^{\mathrm{2}} } \\ $$$${i}\:{will}\:{post}\:{solution}\:{after}\:{i}\:{finish}\:{its}\:\:{not}\:{so}\:{easy} \\ $$$${for}\:{redaction} \\ $$
Commented by mind is power last updated on 06/Apr/20
(1/((x−a_0 ).....(x−a_n )))=Σ_(k=0) ^n (1/(Π_(l=0,l≠k) ^n (a_k −a_l )(x−a_k )))=f(a_0 ,..a_n ) ((∂^(n+1) f(a_0 ,....,a_n ))/(∂a_0 ....∂a_n ))∣_((0,1,,n)) =(1/((x^2 ...(x−n)^2 )) we can see that (∂^(n+1) /(∂a_0 ...∂_a_n ))((1/((x−a_0 ).....(x−a_n ))))=(1/((Π_(k=0) ^n (x−a_k ))^2 )) ∂^(n+1) f(a_0 ,....a_n )= =−Σ_(k=0) ^n .Σ_(j=0,j≠k) ^n (2/((a_k −a_j ).Π_(l=1,l≠k) ^n (a_k −a_l )^2 (x−a_k )))+Σ_(k=0) ^n (1/(Π_(l=0,l≠k) ^n (a_k −a_l )^2 (x−a_k )^2 )) ∂^(n+1) f(0,1,.....,n)= =−Σ_(k=0) ^n (2/(Π_(l=1,l#k) ^n (k−l)^2 )).Σ_(j=0,j≠k) ^n (1/(k−j)).(1/(x−a_k ))+Σ_(k=0) ^n (1/(Π_(l=0,l≠k) ^n (a_k −a_l )^2 (x−a_k )^2 )) =−Σ_(k=0) ^n (2/(Π_(l=0,l≠k) ^n (k−l)^2 )).(H_k −H_(n−k) ).(1/((x−a_k )))+Σ_(k=0) ^n (1/(Π_(l=0,l#k) ^n (k−l)^2 (x−k)^2 )) =Σ_(k=0) ^n ((2(n!)^2 (H_(n−k) −H_k ))/((k)^2 ...(1)....(n−k)^2 .(n!)^2 ))(1/((x−k)))+Σ_(k=0) ^n (((n!)^2 )/((n!)^2 (k...1...(n−k))^2 )).(1/(x−k)) =2Σ_(k=0) ^n (( ((n),(k) )^2 (H_(n−k) −H_k ))/((n!)^2 )).(1/(x−k))+(1/((n!)^2 ))Σ_(k=0) ^n .( ((n),(k) )^2 /((x−k)^2 )) ∫∂^(n+1) f(0,...n)dx=∫(dx/(x^2 (x−1)^2 ...(x−n)^2 )) =2Σ_(k=0) ^n (( ((n),(k) )^2 (H_(n−k) −H_k ))/((n!)^2 )).∫(1/(x−k))dx+(1/((n!)^2 ))Σ_(k=0) ^n ∫.( ((n),(k) )^2 /((x−k)^2 )) (2/((n!)^2 ))Σ_(k=0) ^n ((n),(k) )^2 (H_(n−k) −H_k )ln(x−k)+((Σ_(k=0) ^n ((n),(k) ))/((n!)^2 )).(1/(k−x)) =(1/((n!)^2 ))Σ_(k=0) ^n ( ((n),(k) )^2 /(k−x))+ (2/((n!)^2 ))ln(Π_(k.=0) ^n (x−k)^((H_(n−k) −H_k ) ((n),(k) )^2 ) )+c Σ
$$\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{0}} \right)…..\left({x}−{a}_{{n}} \right)}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\underset{{l}=\mathrm{0},{l}\neq{k}} {\overset{{n}} {\prod}}\left({a}_{{k}} −{a}_{{l}} \right)\left({x}−{a}_{{k}} \right)}={f}\left({a}_{\mathrm{0}} ,..{a}_{{n}} \right) \\ $$$$\frac{\partial^{{n}+\mathrm{1}} {f}\left({a}_{\mathrm{0}} ,….,{a}_{{n}} \right)}{\partial{a}_{\mathrm{0}} ….\partial{a}_{{n}} }\mid_{\left(\mathrm{0},\mathrm{1},,{n}\right)} =\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} …\left({x}−{n}\right)^{\mathrm{2}} \right.}\:\:\:{we}\:{can}\:{see}\:{that} \\ $$$$\frac{\partial^{{n}+\mathrm{1}} }{\partial{a}_{\mathrm{0}} …\partial_{{a}_{{n}} } }\left(\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{0}} \right)…..\left({x}−{a}_{{n}} \right)}\right)=\frac{\mathrm{1}}{\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\left({x}−{a}_{{k}} \right)\right)^{\mathrm{2}} } \\ $$$$\partial^{{n}+\mathrm{1}} {f}\left({a}_{\mathrm{0}} ,….{a}_{{n}} \right)= \\ $$$$=−\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}.\underset{{j}=\mathrm{0},{j}\neq{k}} {\overset{{n}} {\sum}}\frac{\mathrm{2}}{\left({a}_{{k}} −{a}_{{j}} \right).\underset{{l}=\mathrm{1},{l}\neq{k}} {\overset{{n}} {\prod}}\left({a}_{{k}} −{a}_{{l}} \right)^{\mathrm{2}} \left({x}−{a}_{{k}} \right)}+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\underset{{l}=\mathrm{0},{l}\neq{k}} {\overset{{n}} {\prod}}\left({a}_{{k}} −{a}_{{l}} \right)^{\mathrm{2}} \left({x}−{a}_{{k}} \right)^{\mathrm{2}} } \\ $$$$\partial^{{n}+\mathrm{1}} {f}\left(\mathrm{0},\mathrm{1},…..,{n}\right)= \\ $$$$=−\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}}{\underset{{l}=\mathrm{1},{l}#{k}} {\overset{{n}} {\prod}}\left({k}−{l}\right)^{\mathrm{2}} }.\underset{{j}=\mathrm{0},{j}\neq{k}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}−{j}}.\frac{\mathrm{1}}{{x}−{a}_{{k}} }+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\underset{{l}=\mathrm{0},{l}\neq{k}} {\overset{{n}} {\prod}}\left({a}_{{k}} −{a}_{{l}} \right)^{\mathrm{2}} \left({x}−{a}_{{k}} \right)^{\mathrm{2}} } \\ $$$$=−\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}}{\underset{{l}=\mathrm{0},{l}\neq{k}} {\overset{{n}} {\prod}}\left({k}−{l}\right)^{\mathrm{2}} }.\left({H}_{{k}} −{H}_{{n}−{k}} \right).\frac{\mathrm{1}}{\left({x}−{a}_{{k}} \right)}+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\underset{{l}=\mathrm{0},{l}#{k}} {\overset{{n}} {\prod}}\left({k}−{l}\right)^{\mathrm{2}} \left({x}−{k}\right)^{\mathrm{2}} } \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}\left({n}!\right)^{\mathrm{2}} \left({H}_{{n}−{k}} −{H}_{{k}} \right)}{\left({k}\right)^{\mathrm{2}} …\left(\mathrm{1}\right)….\left({n}−{k}\right)^{\mathrm{2}} .\left({n}!\right)^{\mathrm{2}} }\frac{\mathrm{1}}{\left({x}−{k}\right)}+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left({n}!\right)^{\mathrm{2}} }{\left({n}!\right)^{\mathrm{2}} \left({k}…\mathrm{1}…\left({n}−{k}\right)\right)^{\mathrm{2}} }.\frac{\mathrm{1}}{{x}−{k}} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} \left({H}_{{n}−{k}} −{H}_{{k}} \right)}{\left({n}!\right)^{\mathrm{2}} }.\frac{\mathrm{1}}{{x}−{k}}+\frac{\mathrm{1}}{\left({n}!\right)^{\mathrm{2}} }\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}.\frac{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} }{\left({x}−{k}\right)^{\mathrm{2}} } \\ $$$$\int\partial^{{n}+\mathrm{1}} {f}\left(\mathrm{0},…{n}\right){dx}=\int\frac{{dx}}{{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} …\left({x}−{n}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} \left({H}_{{n}−{k}} −{H}_{{k}} \right)}{\left({n}!\right)^{\mathrm{2}} }.\int\frac{\mathrm{1}}{{x}−{k}}{dx}+\frac{\mathrm{1}}{\left({n}!\right)^{\mathrm{2}} }\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\int.\frac{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} }{\left({x}−{k}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{\left({n}!\right)^{\mathrm{2}} }\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} \left({H}_{{n}−{k}} −{H}_{{k}} \right){ln}\left({x}−{k}\right)+\frac{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}}{\left({n}!\right)^{\mathrm{2}} }.\frac{\mathrm{1}}{{k}−{x}} \\ $$$$=\frac{\mathrm{1}}{\left({n}!\right)^{\mathrm{2}} }\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} }{{k}−{x}}+\:\frac{\mathrm{2}}{\left({n}!\right)^{\mathrm{2}} }{ln}\left(\underset{{k}.=\mathrm{0}} {\overset{{n}} {\prod}}\left({x}−{k}\overset{\left({H}_{{n}−{k}} −{H}_{{k}} \right)\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} } {\right)}\right)+{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\Sigma \\ $$
Commented by M±th+et£s last updated on 06/Apr/20
i am speechless sir . god bless you
$${i}\:{am}\:{speechless}\:{sir}\:.\:{god}\:{bless}\:{you} \\ $$
Commented by mind is power last updated on 06/Apr/20
withe pleasur sir ,gold bless You too if you csn reposte somme unswerd Quation may bee i will see somes ideas
$${withe}\:{pleasur}\:{sir}\:,{gold}\:{bless}\:{You}\:{too} \\ $$$${if}\:{you}\:{csn}\:{reposte}\:{somme}\:{unswerd}\:{Quation}\:{may} \\ $$$${bee}\:{i}\:{will}\:{see}\:\:{somes}\:{ideas} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *