Question Number 156475 by SANOGO last updated on 11/Oct/21
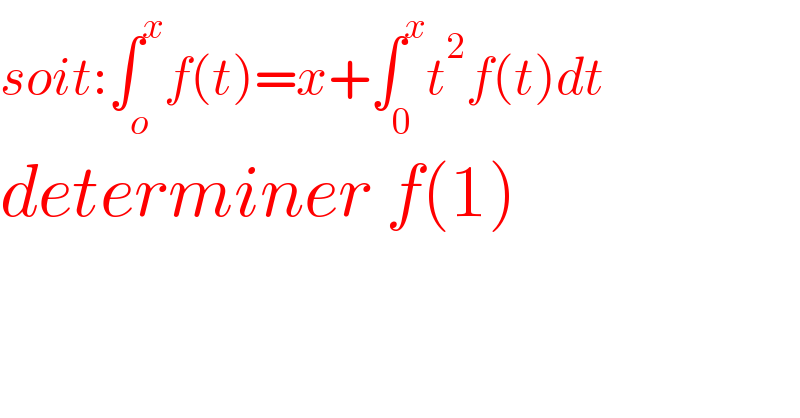
Commented by SANOGO last updated on 11/Oct/21

Commented by mr W last updated on 11/Oct/21

Commented by SANOGO last updated on 11/Oct/21

Commented by mr W last updated on 11/Oct/21
![(d/dx)[∫_(a(x)) ^(b(x)) f(t)dt]=f[b(x)]((db(x))/dx)−f[a(x)]((da(x))/dx)](https://www.tinkutara.com/question/Q156498.png)
Answered by Mathspace last updated on 11/Oct/21

Commented by SANOGO last updated on 11/Oct/21

