Question Number 155101 by SANOGO last updated on 25/Sep/21
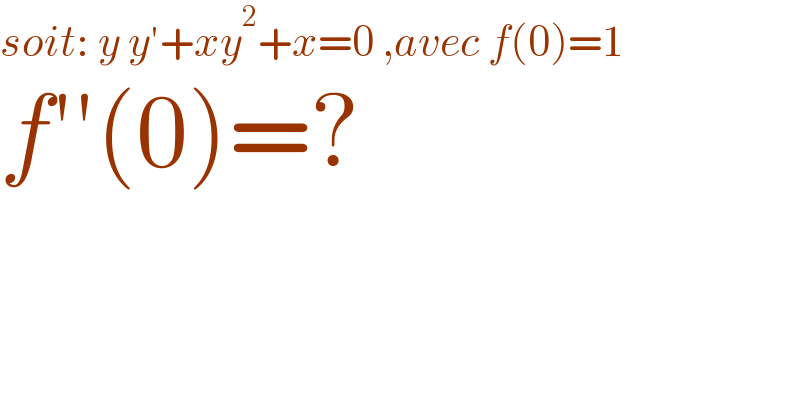
$${soit}:\:{y}\:{y}'+{xy}^{\mathrm{2}} +{x}=\mathrm{0}\:,{avec}\:{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${f}''\left(\mathrm{0}\right)=? \\ $$
Commented by tabata last updated on 25/Sep/21

$$\boldsymbol{{yy}}^{'} \:=\:−\boldsymbol{{x}}\:\left(\boldsymbol{{y}}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:\Rightarrow\:\frac{\boldsymbol{{y}}\:}{\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{1}}\:\boldsymbol{{dy}}\:=\:−\boldsymbol{{x}}\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{{ln}}\:\mid\:\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{1}\mid\:=\:−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\boldsymbol{{c}}}{\mathrm{2}}\:\Rightarrow\:\boldsymbol{{ln}}\:\mid\:\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{1}\mid\:=\:−\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{c}} \\ $$$$ \\ $$$$\boldsymbol{{y}}^{\mathrm{2}} \:=\:\boldsymbol{{k}}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\:\mathrm{1}\:\Rightarrow\:\boldsymbol{{y}}\:=\:\sqrt{\boldsymbol{{k}}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\mathrm{1}} \\ $$$$ \\ $$$$\boldsymbol{{f}}\:\left(\mathrm{0}\right)\:=\:\mathrm{1}\:\Rightarrow\:\mathrm{1}\:=\:\sqrt{\boldsymbol{{k}}\:−\mathrm{1}}\:\Rightarrow\:\boldsymbol{{k}}\:=\:\mathrm{2} \\ $$$$ \\ $$$$\therefore\:\boldsymbol{{y}}\:=\:\sqrt{\mathrm{2}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\mathrm{1}} \\ $$$$ \\ $$$$\boldsymbol{{y}}^{'} \:=\:\frac{−\:\:\mathrm{2}\:\boldsymbol{{x}}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } }{\:\sqrt{\mathrm{2}\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\mathrm{1}}}\:\Rightarrow\:\boldsymbol{{y}}^{''} \:=\:\frac{\left(\sqrt{\mathrm{2}\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\mathrm{1}}\right)\left(\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\mathrm{2}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } \right)−\:\left(\mathrm{2}\:\boldsymbol{{x}}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } \right)\left(\frac{\:\mathrm{2}\:\boldsymbol{{x}}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } }{\:\sqrt{\mathrm{2}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\mathrm{1}}}\right)}{\left(\mathrm{2}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } \:−\:\mathrm{1}\right)} \\ $$$$ \\ $$$$\boldsymbol{{f}}^{\:''} \left(\mathrm{0}\right)\:=\:\frac{\left(\:\sqrt{\mathrm{2}\:−\:\mathrm{1}}\:\right)\:\left(−\:\mathrm{2}\:\right)}{\left(\:\mathrm{2}\:−\:\mathrm{1}\:\right)}\:=\:−\:\frac{\mathrm{2}}{\:\mathrm{1}}\:=\:−\mathrm{2} \\ $$$$ \\ $$$$<\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:> \\ $$
Commented by SANOGO last updated on 25/Sep/21
$${merci}\:{bien} \\ $$
Commented by tabata last updated on 25/Sep/21

$$\boldsymbol{{you}}\:\boldsymbol{{are}}\:\boldsymbol{{welcome}}\: \\ $$
Answered by mr W last updated on 25/Sep/21
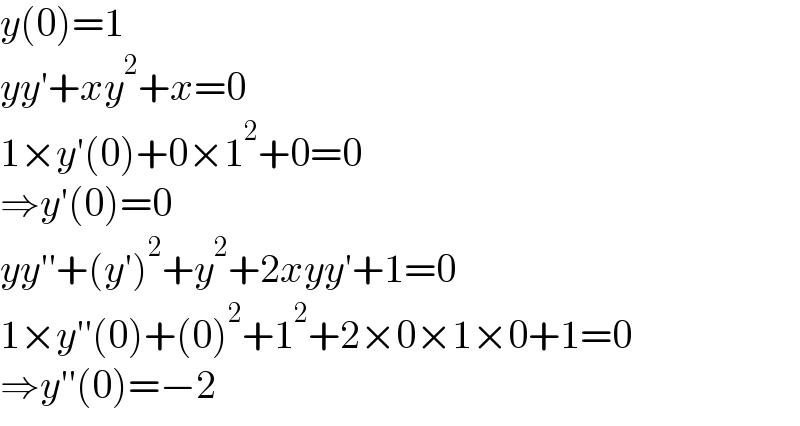
$${y}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${yy}'+{xy}^{\mathrm{2}} +{x}=\mathrm{0} \\ $$$$\mathrm{1}×{y}'\left(\mathrm{0}\right)+\mathrm{0}×\mathrm{1}^{\mathrm{2}} +\mathrm{0}=\mathrm{0} \\ $$$$\Rightarrow{y}'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${yy}''+\left({y}'\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xyy}'+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{1}×{y}''\left(\mathrm{0}\right)+\left(\mathrm{0}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{2}×\mathrm{0}×\mathrm{1}×\mathrm{0}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{y}''\left(\mathrm{0}\right)=−\mathrm{2} \\ $$
Commented by SANOGO last updated on 25/Sep/21
$${merci}\:{bien} \\ $$
