Question Number 35297 by 123 45 polytechnicien last updated on 17/May/18
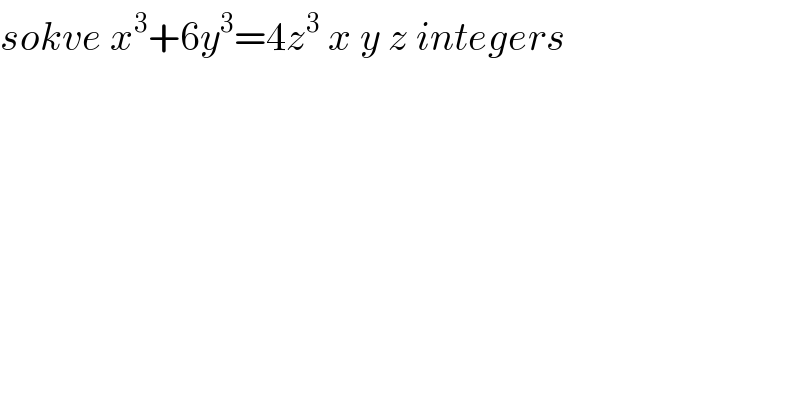
$${sokve}\:{x}^{\mathrm{3}} +\mathrm{6}{y}^{\mathrm{3}} =\mathrm{4}{z}^{\mathrm{3}} \:{x}\:{y}\:{z}\:{integers} \\ $$
Commented by Rasheed.Sindhi last updated on 18/May/18
![4z^3 →even⇒x^3 +6y^3 →even x^3 +6y^3 →even ∧ 6y^3 →even ⇒x^3 →even⇒x→even Let x=2m x^3 +6y^3 =4z^3 ⇒8m^3 +6y^3 =4z^3 ⇒4m^3 +3y^3 =2z^3 4m^3 →even ∧ 2z^3 →even⇒3y^3 →even ⇒y^3 →even⇒y→even x^3 +6y^3 =4z^3 ⇒(even)^3 +6(even)^3 =4z^3 8∣(even)^3 ⇒8∣ [(even)^3 +6(even)^3 ] ⇒8∣4z^3 ⇒z^3 →even⇒z→even So x,y,z→even Let x=2m,y=2n & z=2l x^3 +6y^3 =4z^3 ⇒(2m)^3 +6(2n)^3 =4(2l)^3 8m^3 +6(8n^3 )=4(8l^3 ) m^3 +6n^3 =4l^3 This is same as x^3 +6y^3 =4z^3 (hahaha we reeched at the begning) Anyway we should search x,y,z in in even numbers and this is a clue!](https://www.tinkutara.com/question/Q35388.png)
$$\mathrm{4z}^{\mathrm{3}} \rightarrow\mathrm{even}\Rightarrow\mathrm{x}^{\mathrm{3}} +\mathrm{6y}^{\mathrm{3}} \rightarrow\mathrm{even} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{6y}^{\mathrm{3}} \rightarrow\mathrm{even}\:\wedge\:\mathrm{6y}^{\mathrm{3}} \rightarrow\mathrm{even} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{3}} \rightarrow\mathrm{even}\Rightarrow\mathrm{x}\rightarrow\mathrm{even} \\ $$$$\mathrm{Let}\:\mathrm{x}=\mathrm{2m} \\ $$$${x}^{\mathrm{3}} +\mathrm{6}{y}^{\mathrm{3}} =\mathrm{4}{z}^{\mathrm{3}} \Rightarrow\mathrm{8m}^{\mathrm{3}} +\mathrm{6y}^{\mathrm{3}} =\mathrm{4z}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{4m}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{3}} =\mathrm{2z}^{\mathrm{3}} \\ $$$$\mathrm{4m}^{\mathrm{3}} \rightarrow\mathrm{even}\:\wedge\:\mathrm{2z}^{\mathrm{3}} \rightarrow\mathrm{even}\Rightarrow\mathrm{3y}^{\mathrm{3}} \rightarrow\mathrm{even} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{y}^{\mathrm{3}} \rightarrow\mathrm{even}\Rightarrow\mathrm{y}\rightarrow\mathrm{even} \\ $$$$\:{x}^{\mathrm{3}} +\mathrm{6}{y}^{\mathrm{3}} =\mathrm{4z}^{\mathrm{3}} \Rightarrow\left(\mathrm{even}\right)^{\mathrm{3}} +\mathrm{6}\left(\mathrm{even}\right)^{\mathrm{3}} =\mathrm{4z}^{\mathrm{3}} \\ $$$$\mathrm{8}\mid\left(\mathrm{even}\right)^{\mathrm{3}} \Rightarrow\mathrm{8}\mid\:\left[\left(\mathrm{even}\right)^{\mathrm{3}} +\mathrm{6}\left(\mathrm{even}\right)^{\mathrm{3}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{8}\mid\mathrm{4z}^{\mathrm{3}} \Rightarrow\mathrm{z}^{\mathrm{3}} \rightarrow\mathrm{even}\Rightarrow\mathrm{z}\rightarrow\mathrm{even} \\ $$$$\mathrm{So}\:\mathrm{x},\mathrm{y},\mathrm{z}\rightarrow\mathrm{even} \\ $$$$\mathrm{Let}\:\mathrm{x}=\mathrm{2m},\mathrm{y}=\mathrm{2n}\:\&\:\mathrm{z}=\mathrm{2}{l} \\ $$$${x}^{\mathrm{3}} +\mathrm{6}{y}^{\mathrm{3}} =\mathrm{4}{z}^{\mathrm{3}} \Rightarrow\left(\mathrm{2m}\right)^{\mathrm{3}} +\mathrm{6}\left(\mathrm{2n}\right)^{\mathrm{3}} =\mathrm{4}\left(\mathrm{2}{l}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{8m}^{\mathrm{3}} +\mathrm{6}\left(\mathrm{8n}^{\mathrm{3}} \right)=\mathrm{4}\left(\mathrm{8}{l}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{m}^{\mathrm{3}} +\mathrm{6n}^{\mathrm{3}} =\mathrm{4}{l}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\mathrm{This}\:\mathrm{is}\:\mathrm{same}\:\mathrm{as}\:{x}^{\mathrm{3}} +\mathrm{6}{y}^{\mathrm{3}} =\mathrm{4}{z}^{\mathrm{3}} \\ $$$$\:\:\:\:\left(\boldsymbol{\mathrm{hahaha}}\:\mathrm{we}\:\mathrm{reeched}\:\mathrm{at}\:\mathrm{the}\:\mathrm{begning}\right) \\ $$$$\mathrm{Anyway}\:\mathrm{we}\:\mathrm{should}\:\mathrm{search}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{in} \\ $$$$\mathrm{in}\:\mathrm{even}\:\mathrm{numbers}\:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{clue}! \\ $$
