Menu Close

Solution-from-2xy-dy-x-2-y-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 117632 by syamil last updated on 12/Oct/20
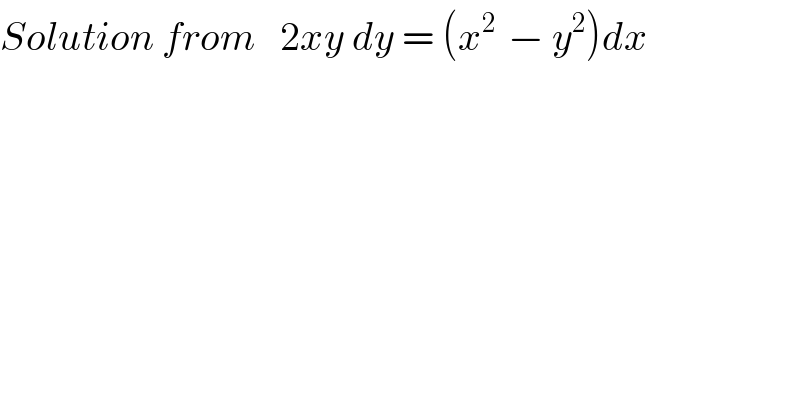
Solution from 2xy dy = (x^(2 ) − y^2 )dx
$${Solution}\:{from}\:\:\:\mathrm{2}{xy}\:{dy}\:=\:\left({x}^{\mathrm{2}\:} \:−\:{y}^{\mathrm{2}} \right){dx} \\ $$
Answered by 1549442205PVT last updated on 13/Oct/20
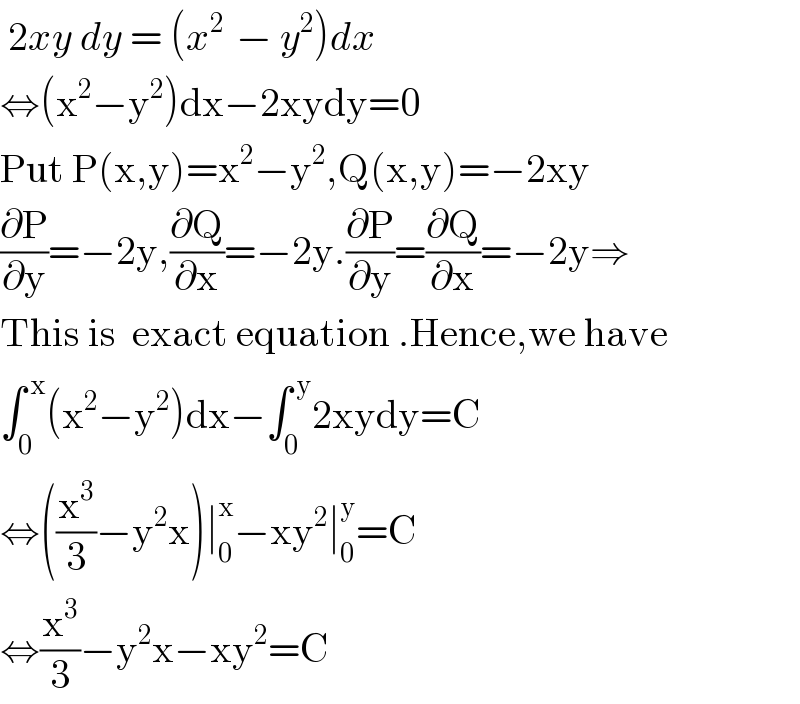
2xy dy = (x^(2 ) − y^2 )dx ⇔(x^2 −y^2 )dx−2xydy=0 Put P(x,y)=x^2 −y^2 ,Q(x,y)=−2xy (∂P/∂y)=−2y,(∂Q/∂x)=−2y.(∂P/∂y)=(∂Q/∂x)=−2y⇒ This is exact equation .Hence,we have ∫_0 ^( x) (x^2 −y^2 )dx−∫_0 ^( y) 2xydy=C ⇔((x^3 /3)−y^2 x)∣_0 ^x −xy^2 ∣_0 ^y =C ⇔(x^3 /3)−y^2 x−xy^2 =C
$$\:\mathrm{2}{xy}\:{dy}\:=\:\left({x}^{\mathrm{2}\:} \:−\:{y}^{\mathrm{2}} \right){dx} \\ $$$$\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)\mathrm{dx}−\mathrm{2xydy}=\mathrm{0} \\ $$$$\mathrm{Put}\:\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} ,\mathrm{Q}\left(\mathrm{x},\mathrm{y}\right)=−\mathrm{2xy} \\ $$$$\frac{\partial\mathrm{P}}{\partial\mathrm{y}}=−\mathrm{2y},\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}=−\mathrm{2y}.\frac{\partial\mathrm{P}}{\partial\mathrm{y}}=\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}=−\mathrm{2y}\Rightarrow \\ $$$$\mathrm{This}\:\mathrm{is}\:\:\mathrm{exact}\:\mathrm{equation}\:.\mathrm{Hence},\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)\mathrm{dx}−\int_{\mathrm{0}} ^{\:\mathrm{y}} \mathrm{2xydy}=\mathrm{C} \\ $$$$\Leftrightarrow\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{y}^{\mathrm{2}} \mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{x}} −\mathrm{xy}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{y}} =\mathrm{C} \\ $$$$\Leftrightarrow\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{y}^{\mathrm{2}} \mathrm{x}−\mathrm{xy}^{\mathrm{2}} =\mathrm{C} \\ $$
Answered by bobhans last updated on 13/Oct/20
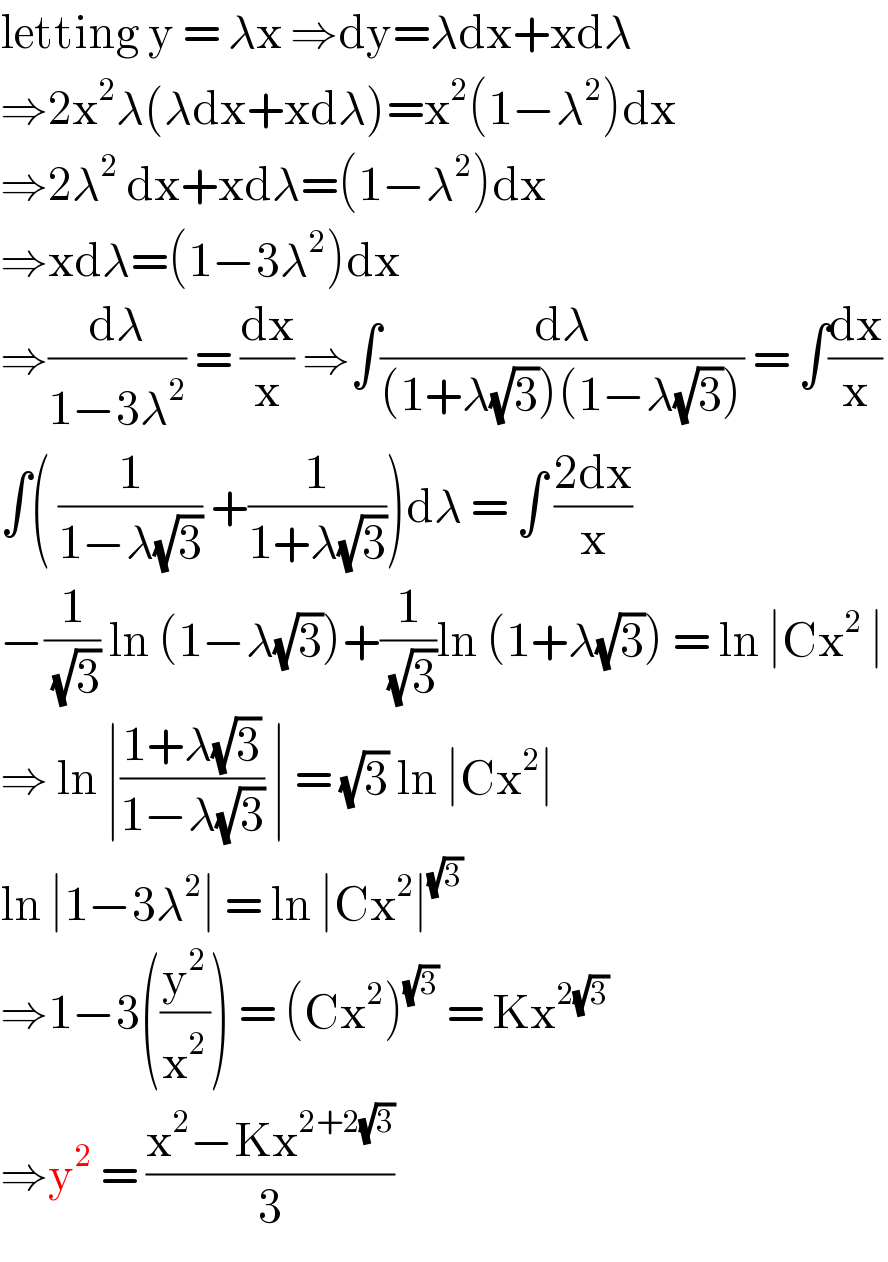
letting y = λx ⇒dy=λdx+xdλ ⇒2x^2 λ(λdx+xdλ)=x^2 (1−λ^2 )dx ⇒2λ^2 dx+xdλ=(1−λ^2 )dx ⇒xdλ=(1−3λ^2 )dx ⇒(dλ/(1−3λ^2 )) = (dx/x) ⇒∫(dλ/((1+λ(√3))(1−λ(√3)))) = ∫(dx/x) ∫( (1/(1−λ(√3))) +(1/(1+λ(√3))))dλ = ∫ ((2dx)/x) −(1/( (√3))) ln (1−λ(√3))+(1/( (√3)))ln (1+λ(√3)) = ln ∣Cx^2 ∣ ⇒ ln ∣((1+λ(√3))/(1−λ(√3))) ∣ = (√3) ln ∣Cx^2 ∣ ln ∣1−3λ^2 ∣ = ln ∣Cx^2 ∣^(√3) ⇒1−3((y^2 /x^2 )) = (Cx^2 )^(√3) = Kx^(2(√3)) ⇒y^2 = ((x^2 −Kx^(2+2(√3)) )/3)
$$\mathrm{letting}\:\mathrm{y}\:=\:\lambda\mathrm{x}\:\Rightarrow\mathrm{dy}=\lambda\mathrm{dx}+\mathrm{xd}\lambda \\ $$$$\Rightarrow\mathrm{2x}^{\mathrm{2}} \lambda\left(\lambda\mathrm{dx}+\mathrm{xd}\lambda\right)=\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\Rightarrow\mathrm{2}\lambda^{\mathrm{2}} \:\mathrm{dx}+\mathrm{xd}\lambda=\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\Rightarrow\mathrm{xd}\lambda=\left(\mathrm{1}−\mathrm{3}\lambda^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\Rightarrow\frac{\mathrm{d}\lambda}{\mathrm{1}−\mathrm{3}\lambda^{\mathrm{2}} }\:=\:\frac{\mathrm{dx}}{\mathrm{x}}\:\Rightarrow\int\frac{\mathrm{d}\lambda}{\left(\mathrm{1}+\lambda\sqrt{\mathrm{3}}\right)\left(\mathrm{1}−\lambda\sqrt{\mathrm{3}}\right)}\:=\:\int\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\int\left(\:\frac{\mathrm{1}}{\mathrm{1}−\lambda\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{1}+\lambda\sqrt{\mathrm{3}}}\right)\mathrm{d}\lambda\:=\:\int\:\frac{\mathrm{2dx}}{\mathrm{x}} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\left(\mathrm{1}−\lambda\sqrt{\mathrm{3}}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{ln}\:\left(\mathrm{1}+\lambda\sqrt{\mathrm{3}}\right)\:=\:\mathrm{ln}\:\mid\mathrm{Cx}^{\mathrm{2}} \:\mid \\ $$$$\Rightarrow\:\mathrm{ln}\:\mid\frac{\mathrm{1}+\lambda\sqrt{\mathrm{3}}}{\mathrm{1}−\lambda\sqrt{\mathrm{3}}}\:\mid\:=\:\sqrt{\mathrm{3}}\:\mathrm{ln}\:\mid\mathrm{Cx}^{\mathrm{2}} \mid\: \\ $$$$\mathrm{ln}\:\mid\mathrm{1}−\mathrm{3}\lambda^{\mathrm{2}} \mid\:=\:\mathrm{ln}\:\mid\mathrm{Cx}^{\mathrm{2}} \mid^{\sqrt{\mathrm{3}}} \: \\ $$$$\Rightarrow\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)\:=\:\left(\mathrm{Cx}^{\mathrm{2}} \right)^{\sqrt{\mathrm{3}}} \:=\:\mathrm{Kx}^{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{2}} \:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{Kx}^{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}} }{\mathrm{3}} \\ $$
Answered by TANMAY PANACEA last updated on 13/Oct/20
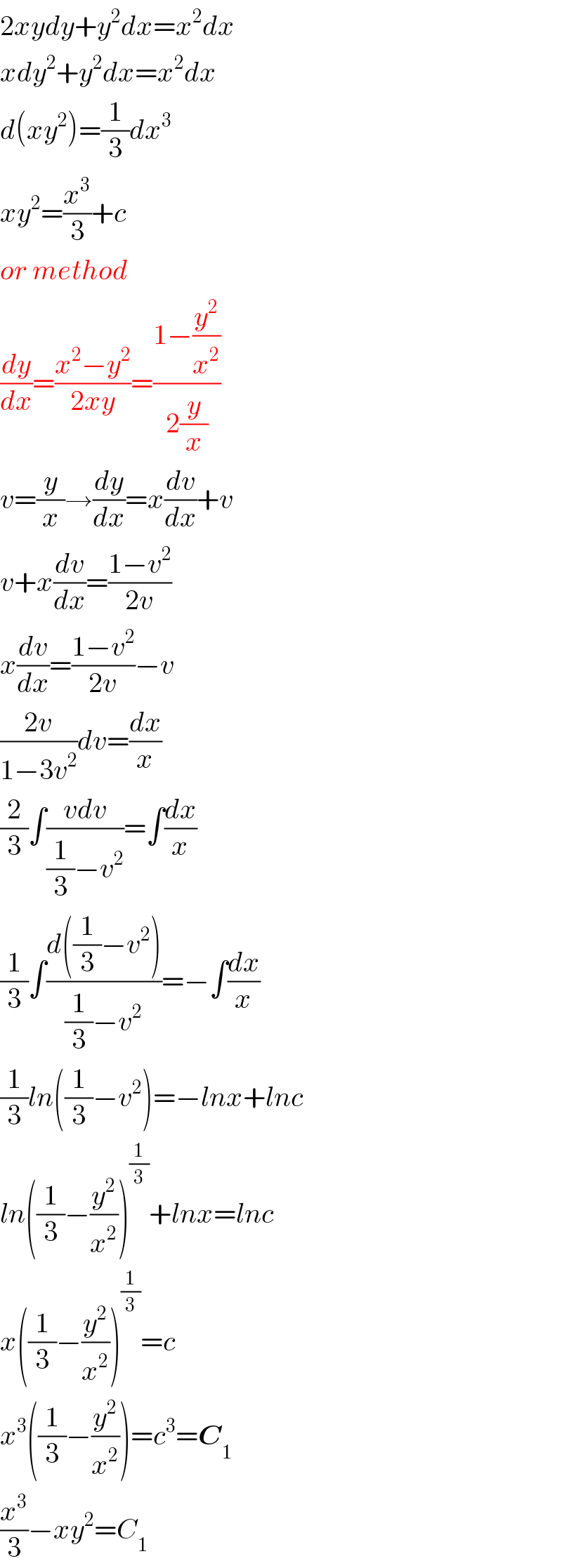
2xydy+y^2 dx=x^2 dx xdy^2 +y^2 dx=x^2 dx d(xy^2 )=(1/3)dx^3 xy^2 =(x^3 /3)+c or method (dy/dx)=((x^2 −y^2 )/(2xy))=((1−(y^2 /x^2 ))/(2(y/x))) v=(y/x)→(dy/dx)=x(dv/dx)+v v+x(dv/dx)=((1−v^2 )/(2v)) x(dv/dx)=((1−v^2 )/(2v))−v ((2v)/(1−3v^2 ))dv=(dx/x) (2/3)∫((vdv)/((1/3)−v^2 ))=∫(dx/x) (1/3)∫((d((1/3)−v^2 ))/((1/3)−v^2 ))=−∫(dx/x) (1/3)ln((1/3)−v^2 )=−lnx+lnc ln((1/3)−(y^2 /x^2 ))^(1/3) +lnx=lnc x((1/3)−(y^2 /x^2 ))^(1/3) =c x^3 ((1/3)−(y^2 /x^2 ))=c^3 =C_1 (x^3 /3)−xy^2 =C_1
$$\mathrm{2}{xydy}+{y}^{\mathrm{2}} {dx}={x}^{\mathrm{2}} {dx} \\ $$$${xdy}^{\mathrm{2}} +{y}^{\mathrm{2}} {dx}={x}^{\mathrm{2}} {dx} \\ $$$${d}\left({xy}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{3}}{dx}^{\mathrm{3}} \\ $$$${xy}^{\mathrm{2}} =\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{c} \\ $$$${or}\:{method} \\ $$$$\frac{{dy}}{{dx}}=\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{\mathrm{2}{xy}}=\frac{\mathrm{1}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}{\mathrm{2}\frac{{y}}{{x}}} \\ $$$${v}=\frac{{y}}{{x}}\rightarrow\frac{{dy}}{{dx}}={x}\frac{{dv}}{{dx}}+{v} \\ $$$${v}+{x}\frac{{dv}}{{dx}}=\frac{\mathrm{1}−{v}^{\mathrm{2}} }{\mathrm{2}{v}} \\ $$$${x}\frac{{dv}}{{dx}}=\frac{\mathrm{1}−{v}^{\mathrm{2}} }{\mathrm{2}{v}}−{v} \\ $$$$\frac{\mathrm{2}{v}}{\mathrm{1}−\mathrm{3}{v}^{\mathrm{2}} }{dv}=\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{vdv}}{\frac{\mathrm{1}}{\mathrm{3}}−{v}^{\mathrm{2}} }=\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{d}\left(\frac{\mathrm{1}}{\mathrm{3}}−{v}^{\mathrm{2}} \right)}{\frac{\mathrm{1}}{\mathrm{3}}−{v}^{\mathrm{2}} }=−\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}−{v}^{\mathrm{2}} \right)=−{lnx}+{lnc} \\ $$$${ln}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +{lnx}={lnc} \\ $$$${x}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ={c} \\ $$$${x}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)={c}^{\mathrm{3}} =\boldsymbol{{C}}_{\mathrm{1}} \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{xy}^{\mathrm{2}} ={C}_{\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *