solve-0-1-dx-x-1-x-

Question Number 118566 by benjo_mathlover last updated on 18/Oct/20

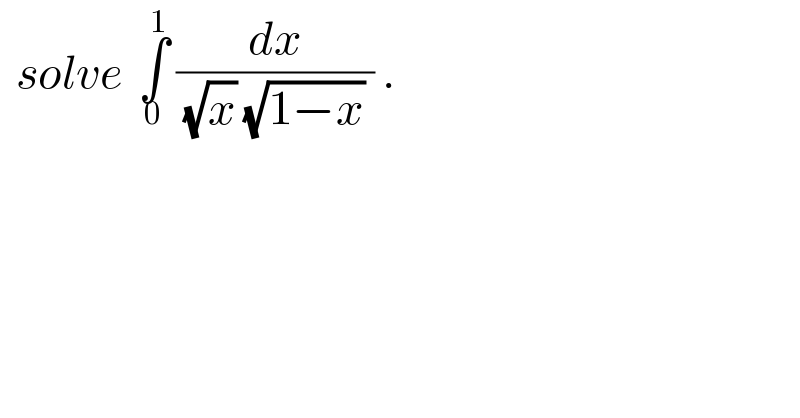
$$\:\:{solve}\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{dx}}{\:\sqrt{{x}}\:\sqrt{\mathrm{1}−{x}}\:}\:. \\ $$

Commented by benjo_mathlover last updated on 18/Oct/20

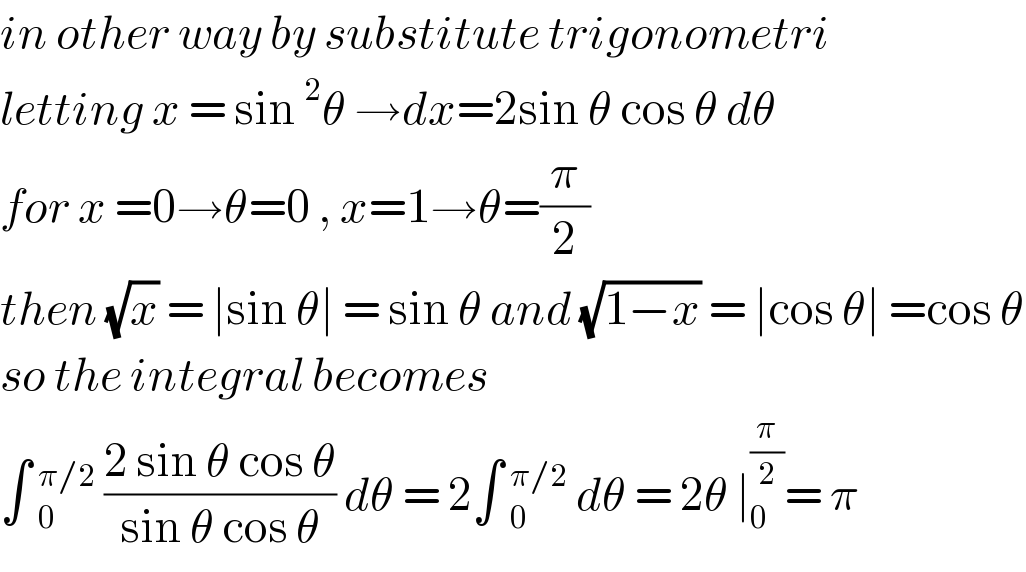
in other way by substitute trigonometri letting x = sin^2 θ →dx=2sin θ cos θ dθ for x =0→θ=0 , x=1→θ=(π/2) then (√x) = ∣sin θ∣ = sin θ and (√(1−x)) = ∣cos θ∣ =cos θ so the integral becomes ∫ _0^(π/2) ((2 sin θ cos θ)/(sin θ cos θ)) dθ = 2∫ _0^(π/2) dθ = 2θ ∣_0 ^(π/2) = π

$${in}\:{other}\:{way}\:{by}\:{substitute}\:{trigonometri} \\ $$$${letting}\:{x}\:=\:\mathrm{sin}\:^{\mathrm{2}} \theta\:\rightarrow{dx}=\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\:{d}\theta \\ $$$${for}\:{x}\:=\mathrm{0}\rightarrow\theta=\mathrm{0}\:,\:{x}=\mathrm{1}\rightarrow\theta=\frac{\pi}{\mathrm{2}} \\ $$$${then}\:\sqrt{{x}}\:=\:\mid\mathrm{sin}\:\theta\mid\:=\:\mathrm{sin}\:\theta\:{and}\:\sqrt{\mathrm{1}−{x}}\:=\:\mid\mathrm{cos}\:\theta\mid\:=\mathrm{cos}\:\theta \\ $$$${so}\:{the}\:{integral}\:{becomes}\: \\ $$$$\int\:_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}\:{d}\theta\:=\:\mathrm{2}\int\:_{\mathrm{0}} ^{\pi/\mathrm{2}} \:{d}\theta\:=\:\mathrm{2}\theta\:\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:\pi \\ $$

Commented by Dwaipayan Shikari last updated on 18/Oct/20

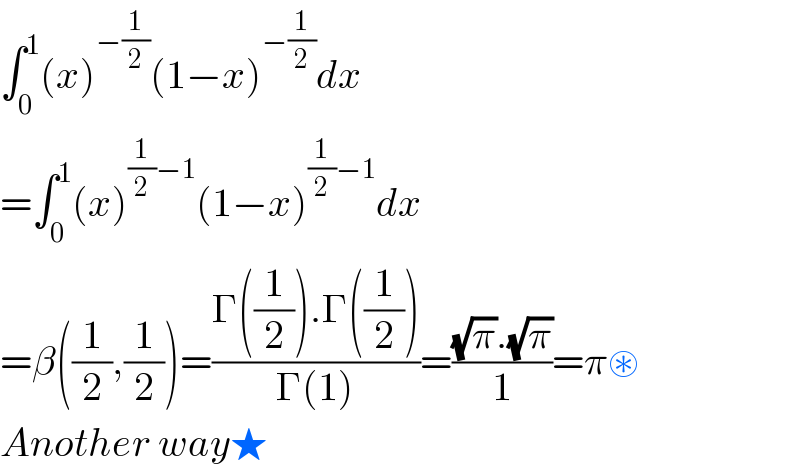
∫_0 ^1 (x)^(−(1/2)) (1−x)^(−(1/2)) dx =∫_0 ^1 (x)^((1/2)−1) (1−x)^((1/2)−1) dx =β((1/2),(1/2))=((Γ((1/2)).Γ((1/2)))/(Γ(1)))=(((√π).(√π))/1)=π⊛ Another way★

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dx} \\ $$$$=\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\sqrt{\pi}.\sqrt{\pi}}{\mathrm{1}}=\pi\circledast \\ $$$${Another}\:{way}\bigstar \\ $$

Answered by TANMAY PANACEA last updated on 18/Oct/20

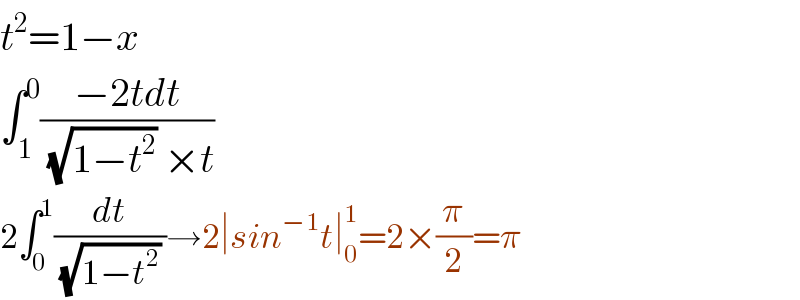
t^2 =1−x ∫_1 ^0 ((−2tdt)/( (√(1−t^2 )) ×t)) 2∫_0 ^1 (dt/( (√(1−t^2 )) ))→2∣sin^(−1) t∣_0 ^1 =2×(π/2)=π

$${t}^{\mathrm{2}} =\mathrm{1}−{x} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{0}} \frac{−\mathrm{2}{tdt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:×{t}} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:}\rightarrow\mathrm{2}\mid{sin}^{−\mathrm{1}} {t}\mid_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}×\frac{\pi}{\mathrm{2}}=\pi \\ $$

Answered by Dwaipayan Shikari last updated on 18/Oct/20

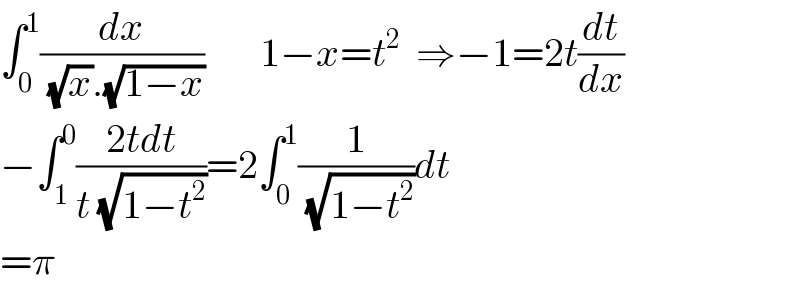
∫_0 ^1 (dx/( (√x).(√(1−x)))) 1−x=t^2 ⇒−1=2t(dt/dx) −∫_1 ^0 ((2tdt)/(t (√(1−t^2 ))))=2∫_0 ^1 (1/( (√(1−t^2 ))))dt =π

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}.\sqrt{\mathrm{1}−{x}}}\:\:\:\:\:\:\:\mathrm{1}−{x}={t}^{\mathrm{2}} \:\:\Rightarrow−\mathrm{1}=\mathrm{2}{t}\frac{{dt}}{{dx}} \\ $$$$−\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{2}{tdt}}{{t}\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt} \\ $$$$=\pi \\ $$

Answered by MJS_new last updated on 18/Oct/20

∫_0 ^1 (dx/( (√x)(√(1−x))))= [t=((√(1−x))/( (√x))) → dx=−2(√x^3 )(√(1−x))dt] =−2∫_(+∞) ^0 (dt/(t^2 +1))=2∫_0 ^(+∞) (dt/(t^2 +1))= =2[arctan t]_0 ^(+∞) =π

$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\:\sqrt{{x}}\sqrt{\mathrm{1}−{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{{x}}}\:\rightarrow\:{dx}=−\mathrm{2}\sqrt{{x}^{\mathrm{3}} }\sqrt{\mathrm{1}−{x}}{dt}\right] \\ $$$$=−\mathrm{2}\underset{+\infty} {\overset{\mathrm{0}} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}\underset{\mathrm{0}} {\overset{+\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\mathrm{2}\left[\mathrm{arctan}\:{t}\right]_{\mathrm{0}} ^{+\infty} =\pi \\ $$

Answered by 1549442205PVT last updated on 18/Oct/20

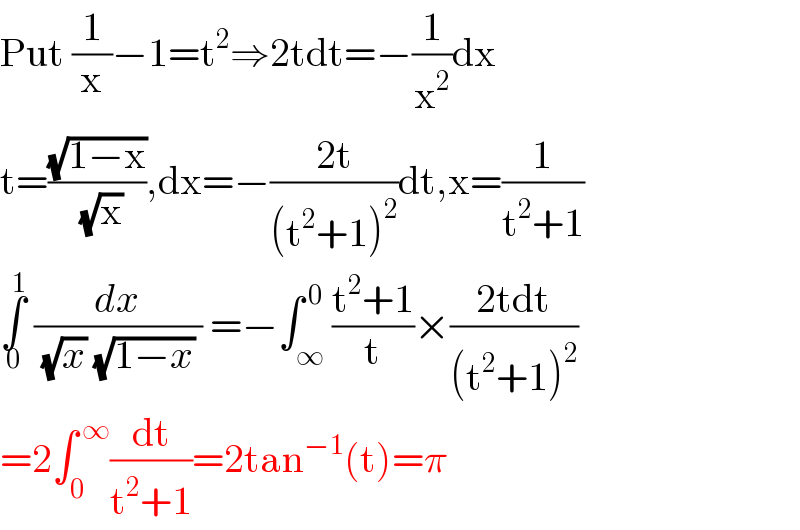
Put (1/x)−1=t^2 ⇒2tdt=−(1/x^2 )dx t=((√(1−x))/( (√x))),dx=−((2t)/((t^2 +1)^2 ))dt,x=(1/(t^2 +1)) ∫_0 ^1 (dx/( (√x) (√(1−x)) )) =−∫_∞ ^( 0) ((t^2 +1)/t)×((2tdt)/((t^2 +1)^2 )) =2∫_0 ^( ∞) (dt/(t^2 +1))=2tan^(−1) (t)=π

$$\mathrm{Put}\:\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}=\mathrm{t}^{\mathrm{2}} \Rightarrow\mathrm{2tdt}=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{t}=\frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\:\sqrt{\mathrm{x}}},\mathrm{dx}=−\frac{\mathrm{2t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt},\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{dx}}{\:\sqrt{{x}}\:\sqrt{\mathrm{1}−{x}}\:}\:=−\int_{\infty} ^{\:\mathrm{0}} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}}×\frac{\mathrm{2tdt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2tan}^{−\mathrm{1}} \left(\mathrm{t}\right)=\pi \\ $$

Commented by MJS_new last updated on 18/Oct/20

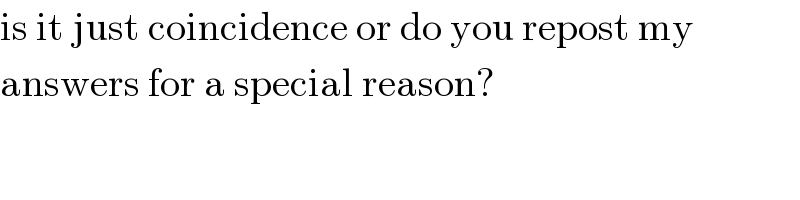
is it just coincidence or do you repost my answers for a special reason?

$$\mathrm{is}\:\mathrm{it}\:\mathrm{just}\:\mathrm{coincidence}\:\mathrm{or}\:\mathrm{do}\:\mathrm{you}\:\mathrm{repost}\:\mathrm{my} \\ $$$$\mathrm{answers}\:\mathrm{for}\:\mathrm{a}\:\mathrm{special}\:\mathrm{reason}? \\ $$

Commented by MJS_new last updated on 18/Oct/20

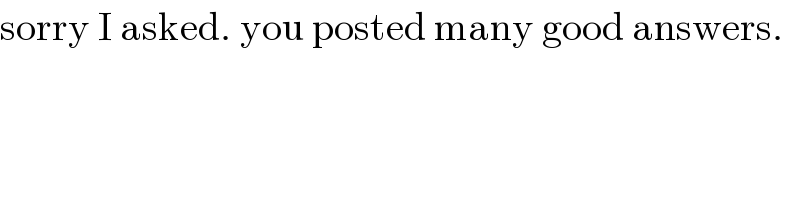
sorry I asked. you posted many good answers.

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{asked}.\:\mathrm{you}\:\mathrm{posted}\:\mathrm{many}\:\mathrm{good}\:\mathrm{answers}. \\ $$

Answered by Bird last updated on 18/Oct/20

I=∫_0 ^1 (dx/( (√x)(√(1−x)))) we do the chang. (√x)=t ⇒I =∫_0 ^1 ((2tdt)/(t(√(1−t^2 )))) =2∫_0 ^1 (dt/( (√(1−t^2 )))) =2[arcsint]_0 ^1 =2×(π/2)=π

$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\:\sqrt{{x}}\sqrt{\mathrm{1}−{x}}}\:{we}\:{do}\:{the}\:{chang}. \\ $$$$\sqrt{{x}}={t}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{tdt}}{{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:=\mathrm{2}\left[{arcsint}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{2}×\frac{\pi}{\mathrm{2}}=\pi \\ $$

Answered by mindispower last updated on 18/Oct/20

=2∫_0 ^1 .(1/(2(√x))).(1/( (√(1−((√x))^2 ))))=2[arcsin((√x))]_0 ^1 =2.(π/2)=1π

$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} .\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\sqrt{{x}}\right)^{\mathrm{2}} }}=\mathrm{2}\left[{arcsin}\left(\sqrt{{x}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}.\frac{\pi}{\mathrm{2}}=\mathrm{1}\pi \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply