Question Number 115215 by mathdave last updated on 24/Sep/20
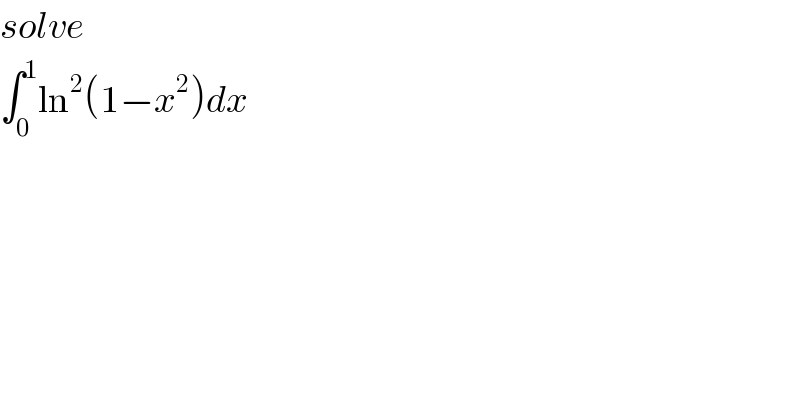
$${solve} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20
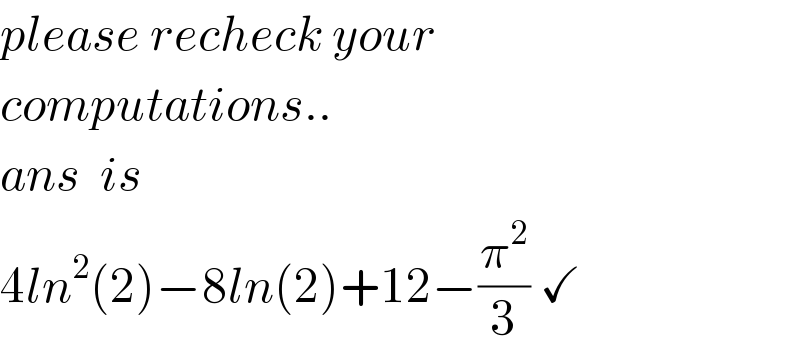
$${please}\:{recheck}\:{your} \\ $$$${computations}.. \\ $$$${ans}\:\:{is} \\ $$$$\mathrm{4}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{8}{ln}\left(\mathrm{2}\right)+\mathrm{12}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\:\checkmark \\ $$
Commented by mathdave last updated on 24/Sep/20

$${that}\:{isnt}\:{the}\:{answer}\:{pls}\:{check}\:{again} \\ $$
Commented by mathdave last updated on 24/Sep/20
Commented by mnjuly1970 last updated on 24/Sep/20
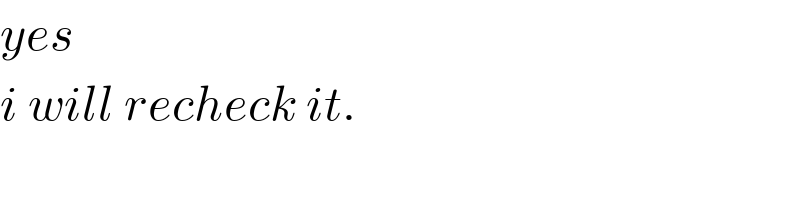
$${yes} \\ $$$${i}\:{will}\:{recheck}\:{it}. \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20

$${difference}\:{is}\:{between} \\ $$$$\mathrm{8}\:\:{and}\:\mathrm{12} \\ $$$${which}\:{is}\:{correct}\:? \\ $$$$\mathrm{8}\:{or}\:\mathrm{12}…. \\ $$$$\:{that}\:{is}\:{very}\:{wonderful} \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20

$${you}\:{are}\:{right}\: \\ $$$${in}\:{my}\:{solution}\: \\ $$$$\:\Omega_{\mathrm{2}\:\:} \:{mus}\:{be}\:\: \\ $$$$\mathrm{2}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{4}{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\: \\ $$$${thank}\:{you}\: \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great} \\ $$
Answered by Bird last updated on 24/Sep/20
![I =∫_0 ^1 ln^2 (1−x^2 )dx by parts I =[(x−1)ln(1−x^2 )]_0 ^1 −∫_0 ^1 (x−1)2ln(1−x^2 )(−2x)dx =4 ∫_0 ^1 x(x−1)ln(1−x^2 )dx we have ln(1−u)^′ =−(1/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ln(1−u)=−Σ_(n=0) ^(∞ ) (u^(n+1) /(n+1))du =−Σ_(n=1) ^∞ (u^n /n) ⇒ I =4∫_0 ^1 (x^2 −x)(−Σ_(n=0) ^∞ (x^(2n) /n)) =−4Σ_(n=1) ^∞ (1/n) ∫_0 ^1 (x^(2n+2) −x^(2n+1) )dx =4{ Σ_(n=1) ^∞ (1/(n(2n+2)))−Σ_(n=1) ^(∞ ) (1/(n(2n+3)))} =lim_(n→+∞) (A_n −B_n ) A_n =(1/2)Σ_(k=1) ^n ((1/n)−(1/(n+1))) =(1/2)(1−(1/2)+(1/2)−(1/3)+...+(1/n)−(1/(n+1))) =(1/2)(n/(n+1)) →(1/2)](https://www.tinkutara.com/question/Q115227.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:\:{by}\:{parts} \\ $$$${I}\:=\left[\left({x}−\mathrm{1}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}−\mathrm{1}\right)\mathrm{2}{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(−\mathrm{2}{x}\right){dx} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left({x}−\mathrm{1}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$$${we}\:{have}\:{ln}\left(\mathrm{1}−{u}\right)^{'} \:=−\frac{\mathrm{1}}{\mathrm{1}−{u}} \\ $$$$=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)=−\sum_{{n}=\mathrm{0}} ^{\infty\:} \frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{du} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow \\ $$$${I}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{2}} −{x}\right)\left(−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}}\right) \\ $$$$=−\mathrm{4}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({x}^{\mathrm{2}{n}+\mathrm{2}} −{x}^{\mathrm{2}{n}+\mathrm{1}} \right){dx} \\ $$$$=\mathrm{4}\left\{\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{2}\right)}−\sum_{{n}=\mathrm{1}} ^{\infty\:} \:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{3}\right)}\right\} \\ $$$$={lim}_{{n}\rightarrow+\infty} \left({A}_{{n}} −{B}_{{n}} \right) \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{{n}}{{n}+\mathrm{1}}\:\rightarrow\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 24/Sep/20

