Question Number 164653 by mnjuly1970 last updated on 20/Jan/22
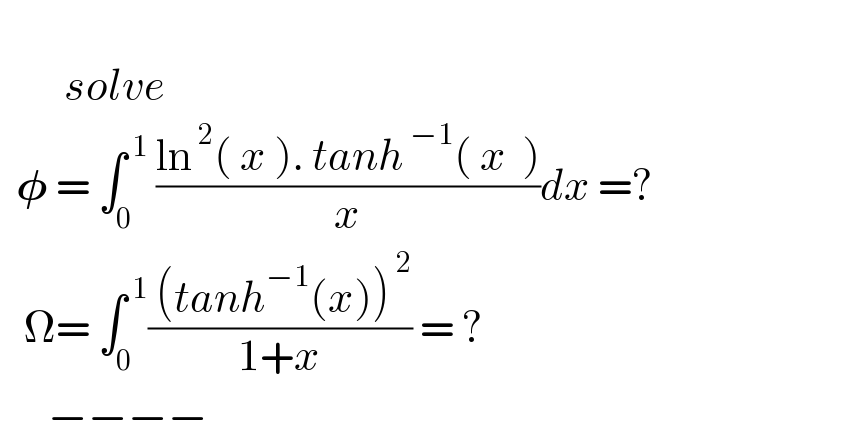
$$ \\ $$$$\:\:\:\:\:\:\:\:{solve} \\ $$$$\:\:\boldsymbol{\phi}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}^{\:\mathrm{2}} \left(\:{x}\:\right).\:{tanh}^{\:−\mathrm{1}} \left(\:{x}\:\:\right)}{{x}}{dx}\:=? \\ $$$$\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\left({tanh}^{−\mathrm{1}} \left({x}\right)\right)^{\:\mathrm{2}} }{\mathrm{1}+{x}}\:=\:? \\ $$$$\:\:\:\:\:\:−−−− \\ $$
Answered by Lordose last updated on 20/Jan/22
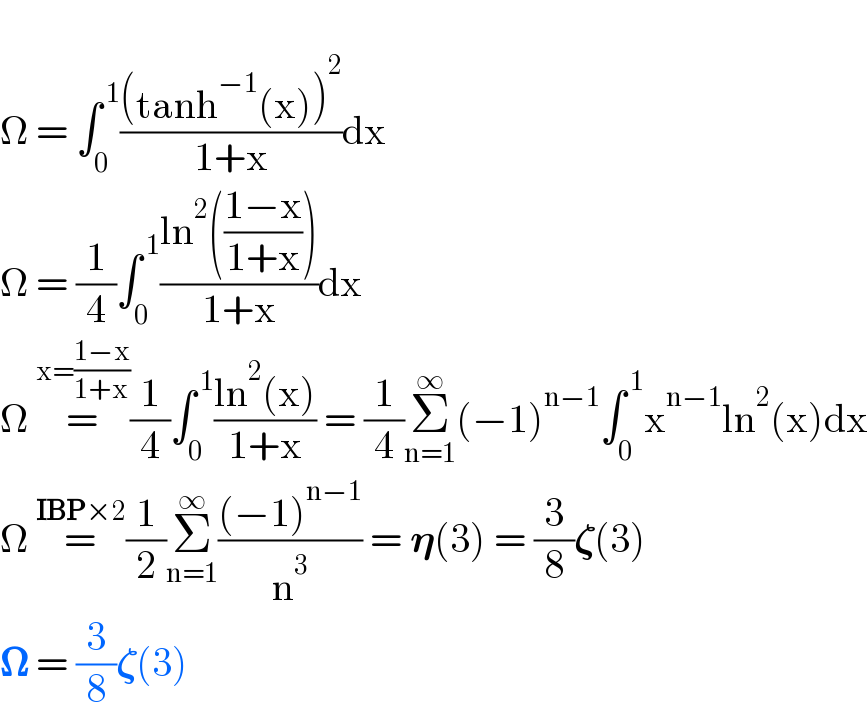
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{tanh}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{x}=\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}} {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\Omega\:\overset{\boldsymbol{\mathrm{IBP}}×\mathrm{2}} {=}\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{3}} }\:=\:\boldsymbol{\eta}\left(\mathrm{3}\right)\:=\:\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$$$\boldsymbol{\Omega}\:=\:\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{\zeta}\left(\mathrm{3}\right)\: \\ $$
Answered by Ar Brandon last updated on 20/Jan/22
![φ=∫_0 ^1 ((ln^2 xtanh^(−1) (x))/x)dx =[((ln^3 x)/3)tanh^(−1) (x)]_0 ^1 −(1/3)∫_0 ^1 ((ln^3 x)/(1−x^2 ))dx =−(1/3)∙(1/2)∙(1/8)∫_0 ^1 ((u^(−(1/2)) ln^3 u)/(1−u))du=(1/(48))ψ^((3)) ((1/2)) =2(ζ(4)−(1/(16))ζ(4))=((15)/8)ζ(4)=((15)/(720))π^4](https://www.tinkutara.com/question/Q164666.png)
$$ \\ $$$$\phi=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} {x}\mathrm{tanh}^{−\mathrm{1}} \left({x}\right)}{{x}}{dx} \\ $$$$\:\:\:=\left[\frac{\mathrm{ln}^{\mathrm{3}} {x}}{\mathrm{3}}\mathrm{tanh}^{−\mathrm{1}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} {x}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{ln}^{\mathrm{3}} {u}}{\mathrm{1}−{u}}{du}=\frac{\mathrm{1}}{\mathrm{48}}\psi^{\left(\mathrm{3}\right)} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\mathrm{2}\left(\zeta\left(\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{16}}\zeta\left(\mathrm{4}\right)\right)=\frac{\mathrm{15}}{\mathrm{8}}\zeta\left(\mathrm{4}\right)=\frac{\mathrm{15}}{\mathrm{720}}\pi^{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 20/Jan/22
$$\:\:{verh}\:{nice}\:…{thank}\:{you} \\ $$$${sir}\:{brandon}… \\ $$
