Question Number 118466 by mathdave last updated on 17/Oct/20
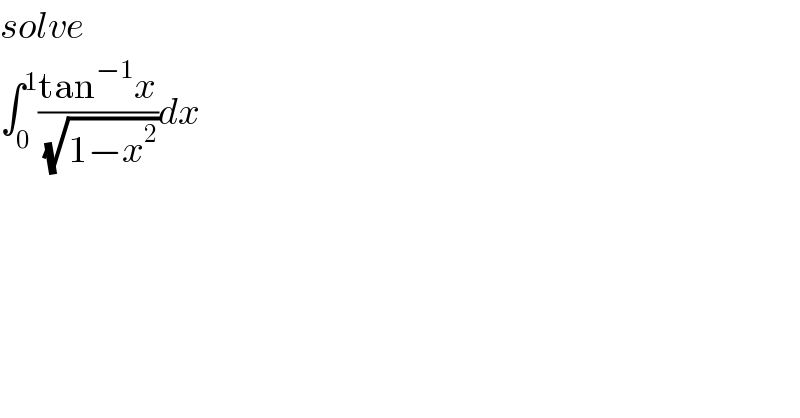
$${solve} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$
Answered by mathmax by abdo last updated on 17/Oct/20
![let take a try with series I =∫_0 ^1 ((arctanx)/( (√(1−x^2 ))))dx changement x=sint give I =∫_0 ^(π/2) ((arctan(sint))/(cost))cost dt =∫_0 ^(π/2) arctan(sint)dt =[t arctan(sint)]_0 ^(π/2) −∫_0 ^(π/2) t .((cost)/(1+sin^2 t))dt =(π^2 /8)−∫_0 ^(π/2) ((t cost)/(1+sin^2 t))dt chang. tan((t/2))=u give ∫_0 ^(π/2) ((t cost)/(1+sin^2 t))dt =∫_0 ^1 ((2 arctanu×((1−u^2 )/(1+u^2 )))/(1+((4u^2 )/(1+u^2 ))))×((2du)/(1+u^2 )) =4 ∫_0 ^1 (((1−u^2 )arctanu)/((1+u^2 )( 1+u^2 +4u^2 )))du =4 ∫_0 ^1 (((1−u^2 )arctanu)/((u^2 +1)(5u^2 +1)))du =(4/5)×((−5)/4)∫_0 ^1 (1−u^2 )arctanu{(1/(u^2 +1))−(1/(u^2 +(1/5)))}du =∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du−∫_0 ^1 (((u^2 −1)arctanu)/(u^2 +(1/5)))du ∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du =∫_0 ^1 (u^2 −1)arctanu(Σ_(n=0) ^∞ (−1)^n u^(2n) )du =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 (u^(2n+2) −u^(2n) )arctanu du =Σ_(n=0) ^∞ (−1)^n U_n U_n =∫_0 ^1 (u^(2n+2) −u^(2n) )arctanu du=[((u^(2n+3) /(2n+3))−(u^(2n+1) /(2n+1)))arctanu]_0 ^1 −∫_0 ^1 ((u^(2n+3) /(2n+3))−(u^(2n+1) /(2n+1)))(du/(1+u^2 )) =(π/4)((1/(2n+3))−(1/(2n+1))) +(1/(2n+1))∫_0 ^1 (u^(2n+1) /(1+u^2 ))du−(1/(2n+3))∫_0 ^1 (u^(2n+3) /(1+u^2 ))du also ∫_0 ^1 (u^(2n+1) /(1+u^2 ))du =∫_0 ^1 u^(2n+1) Σ_(p=0) ^∞ (−1)^p u^(2p) =Σ_(p=0) ^∞ (−1)^p ∫_0 ^1 u^(2n+2p+1) =Σ_(p=0) ^∞ (((−1)^p )/(2n+2p+2)) and ∫_0 ^1 (u^(2n+3) /(1+u^2 ))du =Σ_(p=0) ^∞ (((−1)^p )/(2n+2p +4)) ⇒ U_n =(π/4)((1/(2n+3))−(1/(2n+1)))+(1/(2(2n+1)))Σ_(p=0) ^∞ (((−1)^p )/(n+p+1)) −(1/(2(2n+3)))Σ_(p=0) ^∞ (((−1)^p )/(n+p+2)) ⇒ ∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du =(π/4)Σ_(n=0) ^∞ (((−1)^n )/(2n+3))−(π/4)Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) +(1/2)Σ_(n=0) ^∞ (Σ_(p=0) ^∞ (((−1)^p )/((2n+1)(n+p+1))))−(1/2)Σ_(n=0) ^∞ (Σ_(p=0) ^∞ (((−1)^p )/((2n+3)(n+p+2)))) ...be continued...](https://www.tinkutara.com/question/Q118472.png)
$$\mathrm{let}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{with}\:\mathrm{series}\:\:\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{arctanx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{sint}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{arctan}\left(\mathrm{sint}\right)}{\mathrm{cost}}\mathrm{cost}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{arctan}\left(\mathrm{sint}\right)\mathrm{dt} \\ $$$$=\left[\mathrm{t}\:\mathrm{arctan}\left(\mathrm{sint}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\mathrm{t}\:.\frac{\mathrm{cost}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{t}\:\mathrm{cost}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}\:\:\mathrm{chang}.\:\:\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{t}\:\mathrm{cost}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}\:\mathrm{arctanu}×\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{4u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}×\frac{\mathrm{2du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\mathrm{arctanu}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\:\:\mathrm{1}+\mathrm{u}^{\mathrm{2}} \:+\mathrm{4u}^{\mathrm{2}} \right)}\mathrm{du}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \:\right)\mathrm{arctanu}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{5u}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{du} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}×\frac{−\mathrm{5}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\mathrm{arctanu}\left\{\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{5}}}\right\}\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{arctanu}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{arctanu}}{\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{5}}}\mathrm{du} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{arctanu}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{arctanu}\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{2n}} \right)\mathrm{du} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{u}^{\mathrm{2n}+\mathrm{2}} −\mathrm{u}^{\mathrm{2n}} \right)\mathrm{arctanu}\:\mathrm{du}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{U}_{\mathrm{n}} \\ $$$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{u}^{\mathrm{2n}+\mathrm{2}} −\mathrm{u}^{\mathrm{2n}} \right)\mathrm{arctanu}\:\mathrm{du}=\left[\left(\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{3}} }{\mathrm{2n}+\mathrm{3}}−\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\right)\mathrm{arctanu}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{3}} }{\mathrm{2n}+\mathrm{3}}−\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\right)\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right)\:+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{3}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:\mathrm{also} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{\mathrm{2n}+\mathrm{1}} \sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{p}} \:\mathrm{u}^{\mathrm{2p}} =\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{p}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{\mathrm{2n}+\mathrm{2p}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\mathrm{2n}+\mathrm{2p}+\mathrm{2}}\:\mathrm{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{2n}+\mathrm{3}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\mathrm{2n}+\mathrm{2p}\:+\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{U}_{\mathrm{n}} =\frac{\pi}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2n}+\mathrm{1}\right)}\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\mathrm{n}+\mathrm{p}+\mathrm{1}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2n}+\mathrm{3}\right)}\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\mathrm{n}+\mathrm{p}+\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{arctanu}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\frac{\pi}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{3}}−\frac{\pi}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\left(\mathrm{2n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{p}+\mathrm{2}\right)}\right) \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by TANMAY PANACEA last updated on 17/Oct/20
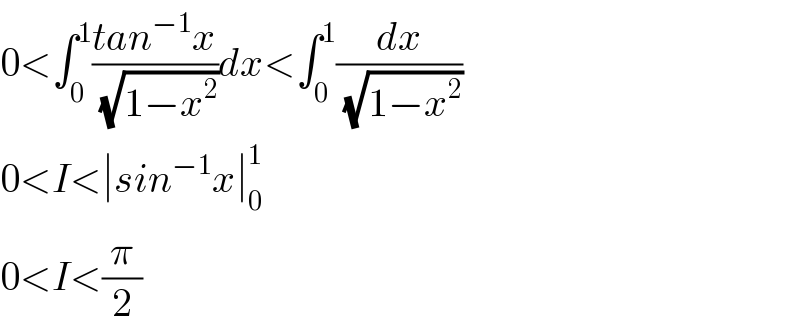
$$\mathrm{0}<\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tan}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}<\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{0}<{I}<\mid{sin}^{−\mathrm{1}} {x}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{0}<{I}<\frac{\pi}{\mathrm{2}} \\ $$
