Question Number 122406 by mathdave last updated on 16/Nov/20
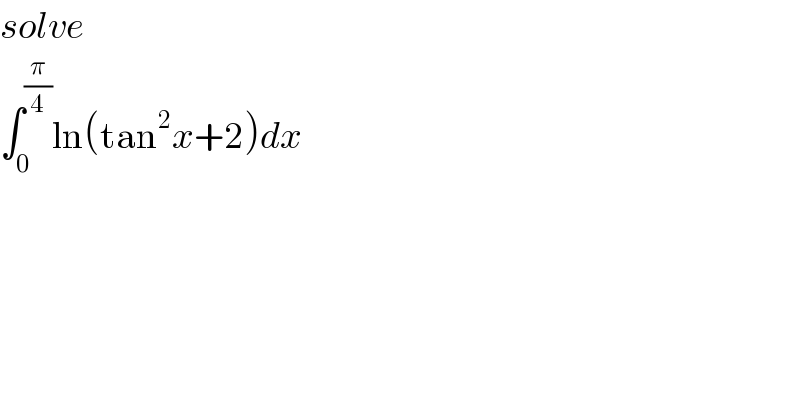
$${solve} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{tan}^{\mathrm{2}} {x}+\mathrm{2}\right){dx} \\ $$
Answered by TANMAY PANACEA last updated on 16/Nov/20
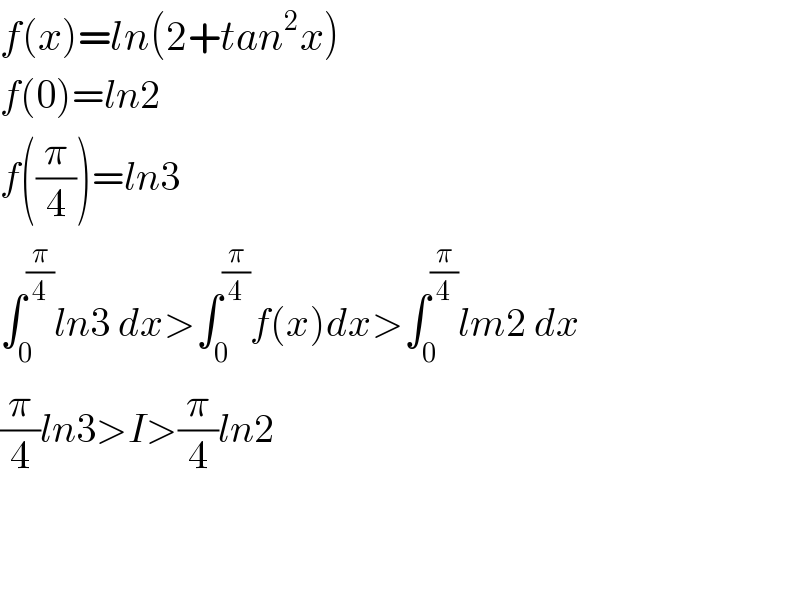
$${f}\left({x}\right)={ln}\left(\mathrm{2}+{tan}^{\mathrm{2}} {x}\right) \\ $$$${f}\left(\mathrm{0}\right)={ln}\mathrm{2} \\ $$$${f}\left(\frac{\pi}{\mathrm{4}}\right)={ln}\mathrm{3} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{3}\:{dx}>\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {f}\left({x}\right){dx}>\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lm}\mathrm{2}\:{dx} \\ $$$$\frac{\pi}{\mathrm{4}}{ln}\mathrm{3}>{I}>\frac{\pi}{\mathrm{4}}{ln}\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 16/Nov/20

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{cosx}\right)\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\mathrm{ln}\left(\mathrm{3}+\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx}−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{3}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx}−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx}=_{\mathrm{2x}=\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cost}\right)\mathrm{dt}\:\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{acost}\right)\mathrm{dt}\:\:\mathrm{with}\:\mathrm{0}<\mathrm{a}<\mathrm{1} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cost}}{\mathrm{1}+\mathrm{acost}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{acost}−\mathrm{1}}{\mathrm{1}+\mathrm{acost}}\mathrm{dt} \\ $$$$=\frac{\pi}{\mathrm{2a}}−\frac{\mathrm{1}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{acost}}\left(\rightarrow\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}\right) \\ $$$$=\frac{\pi}{\mathrm{2a}}−\frac{\mathrm{1}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{a}\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)}=\frac{\pi}{\mathrm{2a}}−\frac{\mathrm{2}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} +\mathrm{a}−\mathrm{au}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2a}}−\frac{\mathrm{2}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{a}+\left(\mathrm{1}−\mathrm{a}\right)\mathrm{u}^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{2}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{a}\:+\left(\mathrm{1}−\mathrm{a}\right)\mathrm{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}+\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\mathrm{u}^{\mathrm{2}} } \\ $$$$=_{\sqrt{\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}}\mathrm{u}=\mathrm{z}} \:\:\:\:\frac{\mathrm{2}}{\mathrm{a}\left(\mathrm{1}+\mathrm{a}\right)}\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{1}+\mathrm{a}}}{\:\sqrt{\mathrm{1}−\mathrm{a}}}\mathrm{dz} \\ $$$$=\frac{\mathrm{2}}{\mathrm{a}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\mathrm{arctan}\left(\sqrt{\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{2}}\mathrm{lna}−\mathrm{2}\int\:\:\frac{\mathrm{arctan}\left(\sqrt{\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}}\right)}{\mathrm{a}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\mathrm{da}\:+\mathrm{c} \\ $$$$\int\:\:\:\frac{\mathrm{arctan}\left(\sqrt{\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}}\right)}{\mathrm{a}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\mathrm{da}\:=_{\mathrm{a}=\mathrm{cos}\theta} \:\:\:\:\int\:\:\frac{\mathrm{arctan}\left(\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)\right)}{\mathrm{cos}\theta\:.\mathrm{sin}\theta}\:\mathrm{sin}\theta\:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\:\:\frac{\theta}{\mathrm{cos}\theta}\mathrm{d}\theta…..\mathrm{be}\:\mathrm{continued}…. \\ $$
