Question Number 118242 by mathdave last updated on 16/Oct/20
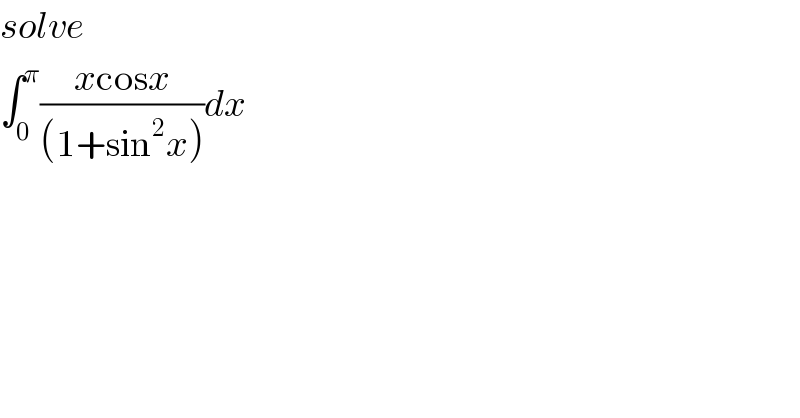
$${solve} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{x}\mathrm{cos}{x}}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}\right)}{dx} \\ $$
Answered by TANMAY PANACEA last updated on 16/Oct/20
![★∫((cosx)/(1+sin^2 x))dx=∫((d(sinx))/(1+sin^2 x))=tan^(−1) (sinx)★ now ∫_0 ^π ((xcosx)/(1+sin^2 x))dx ∣xtan^(−1) (sinx)∣_0 ^π −∫_0 ^π 1×tan^(−1) (sinx)dx 0−∫_0 ^π tan^(−1) (sinx)dx f(x)=tan^(−1) (sinx) f(0)=0 f(π)=0 so tan^(−1) (sinx) make a loop in x∈ [0,π] in between [0,π] tan^(−1) (sinx) must have maximum value ...at x=(π/2) tan^(−1) (sin(π/2))=(π/4) ∫_0 ^π (π/4)dx>∫_0 ^π tan^(−1) (sinx)dx>0 (π^2 /4)>∫_0 ^π tan^(−1) (sinx)dx>0 (−1)(π^2 /4)<∫_0 ^π −tan^(−1) (sinx)dx<0 so I=∫_0 ^π ((xcosx)/((1+sin^2 x)))=∫_0 ^π −tan^(−1) (sinx)dx ((−π^2 )/4)<I<0](https://www.tinkutara.com/question/Q118320.png)
$$\bigstar\int\frac{{cosx}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}{dx}=\int\frac{{d}\left({sinx}\right)}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}={tan}^{−\mathrm{1}} \left({sinx}\right)\bigstar \\ $$$${now} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{xcosx}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}{dx} \\ $$$$\mid{xtan}^{−\mathrm{1}} \left({sinx}\right)\mid_{\mathrm{0}} ^{\pi} −\int_{\mathrm{0}} ^{\pi} \mathrm{1}×{tan}^{−\mathrm{1}} \left({sinx}\right){dx} \\ $$$$\mathrm{0}−\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left({sinx}\right){dx} \\ $$$${f}\left({x}\right)={tan}^{−\mathrm{1}} \left({sinx}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left(\pi\right)=\mathrm{0} \\ $$$${so}\:{tan}^{−\mathrm{1}} \left({sinx}\right)\:\:{make}\:{a}\:{loop}\:{in}\:{x}\in\:\left[\mathrm{0},\pi\right] \\ $$$${in}\:{between}\:\left[\mathrm{0},\pi\right]\:{tan}^{−\mathrm{1}} \left({sinx}\right)\:{must}\:{have}\:{maximum} \\ $$$${value}\:…{at}\:{x}=\frac{\pi}{\mathrm{2}}\:\:\:\:\:{tan}^{−\mathrm{1}} \left({sin}\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}} \\ $$$$\:\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{4}}{dx}>\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left({sinx}\right){dx}>\mathrm{0} \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{4}}>\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left({sinx}\right){dx}>\mathrm{0} \\ $$$$\left(−\mathrm{1}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{4}}<\int_{\mathrm{0}} ^{\pi} −{tan}^{−\mathrm{1}} \left({sinx}\right){dx}<\mathrm{0} \\ $$$${so}\:{I}=\int_{\mathrm{0}} ^{\pi} \frac{{xcosx}}{\left(\mathrm{1}+{sin}^{\mathrm{2}} {x}\right)}=\int_{\mathrm{0}} ^{\pi} −{tan}^{−\mathrm{1}} \left({sinx}\right){dx} \\ $$$$\frac{−\pi^{\mathrm{2}} }{\mathrm{4}}<{I}<\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
