solve-0-sin-3-x-cos-2-x-x-3-dx-7pi-32-

Question Number 152061 by mnjuly1970 last updated on 25/Aug/21

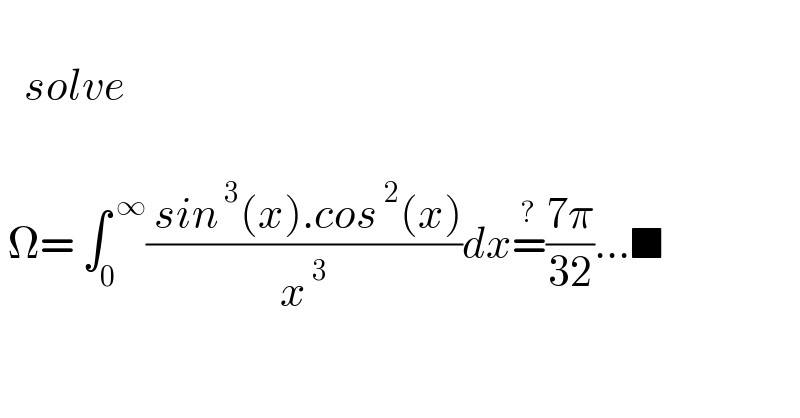
solve Ω= ∫_0 ^( ∞) (( sin^( 3) (x).cos^( 2) (x))/x^( 3) )dx=^? ((7π)/(32))...■

$$ \\ $$$$\:\:\:{solve} \\ $$$$\:\:\:\: \\ $$$$\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}^{\:\mathrm{3}} \left({x}\right).{cos}^{\:\mathrm{2}} \left({x}\right)}{{x}^{\:\mathrm{3}} }{dx}\overset{?} {=}\frac{\mathrm{7}\pi}{\mathrm{32}}…\blacksquare \\ $$

Answered by Ar Brandon last updated on 25/Aug/21

Ω=∫_0 ^∞ ((sin^3 xcos^2 x)/x^3 )dx=∫_0 ^∞ ((sin^3 x−sin^5 x)/x^3 )dx −8isin^3 x=(e^(ix) −e^(−ix) )^3 =e^(3ix) −3e^(ix) +3e^(−ix) −e^(3ix) sin^3 x=(3/4)sinx−(1/4)sin3x 32isin^5 x=(e^(ix) −e^(−ix) )^5 =e^(5ix) −5e^(3ix) +10e^(ix) −10e^(−ix) +5e^(−3ix) −e^(−5ix) sin^5 x=(1/(16))sin5x−(5/(16))sin3x+(5/8)sinx Ω=∫_0 ^∞ ((1/8)∙((sinx)/x^3 )+(1/(16))∙((sin3x)/x^3 )−(1/(16))∙((sin5x)/x^3 ))dx =(1/8)∙(π/(2Γ(3)sin(((3π)/2))))+(1/(16))∙((π×3^2 )/(2Γ(3)sin(((3π)/2))))−(1/(16))∙((π×5^2 )/(2Γ(3)sin(((3π)/2)))) =−(π/(32))−((9π)/(64))+((25π)/(64))=((−2π−9π+25π)/(64))=((14π)/(64))=((7π)/(32))★

$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} {x}\mathrm{cos}^{\mathrm{2}} {x}}{{x}^{\mathrm{3}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} {x}−\mathrm{sin}^{\mathrm{5}} {x}}{{x}^{\mathrm{3}} }{dx} \\ $$$$−\mathrm{8}{i}\mathrm{sin}^{\mathrm{3}} {x}=\left({e}^{{ix}} −{e}^{−{ix}} \right)^{\mathrm{3}} ={e}^{\mathrm{3}{ix}} −\mathrm{3}{e}^{{ix}} +\mathrm{3}{e}^{−{ix}} −{e}^{\mathrm{3}{ix}} \\ $$$$\mathrm{sin}^{\mathrm{3}} {x}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}{x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin3}{x} \\ $$$$\mathrm{32}{i}\mathrm{sin}^{\mathrm{5}} {x}=\left({e}^{{ix}} −{e}^{−{ix}} \right)^{\mathrm{5}} ={e}^{\mathrm{5}{ix}} −\mathrm{5}{e}^{\mathrm{3}{ix}} +\mathrm{10}{e}^{{ix}} −\mathrm{10}{e}^{−{ix}} +\mathrm{5}{e}^{−\mathrm{3}{ix}} −{e}^{−\mathrm{5}{ix}} \\ $$$$\mathrm{sin}^{\mathrm{5}} {x}=\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin5}{x}−\frac{\mathrm{5}}{\mathrm{16}}\mathrm{sin3}{x}+\frac{\mathrm{5}}{\mathrm{8}}\mathrm{sin}{x} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\mathrm{sin}{x}}{{x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{16}}\centerdot\frac{\mathrm{sin3}{x}}{{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{16}}\centerdot\frac{\mathrm{sin5}{x}}{{x}^{\mathrm{3}} }\right){dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\pi}{\mathrm{2}\Gamma\left(\mathrm{3}\right)\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)}+\frac{\mathrm{1}}{\mathrm{16}}\centerdot\frac{\pi×\mathrm{3}^{\mathrm{2}} }{\mathrm{2}\Gamma\left(\mathrm{3}\right)\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{\mathrm{16}}\centerdot\frac{\pi×\mathrm{5}^{\mathrm{2}} }{\mathrm{2}\Gamma\left(\mathrm{3}\right)\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:=−\frac{\pi}{\mathrm{32}}−\frac{\mathrm{9}\pi}{\mathrm{64}}+\frac{\mathrm{25}\pi}{\mathrm{64}}=\frac{−\mathrm{2}\pi−\mathrm{9}\pi+\mathrm{25}\pi}{\mathrm{64}}=\frac{\mathrm{14}\pi}{\mathrm{64}}=\frac{\mathrm{7}\pi}{\mathrm{32}}\bigstar \\ $$

Commented by mnjuly1970 last updated on 25/Aug/21

$${thanks}\:{alot}\:{master}\:{brandon} \\ $$

Commented by Ar Brandon last updated on 25/Aug/21

$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{Sir}\:! \\ $$

Facebook Tweet Pin

solve-0-sin-3-x-cos-2-x-x-3-dx-7pi-32-

Leave a Reply Cancel reply