Question Number 15656 by Tinkutara last updated on 12/Jun/17
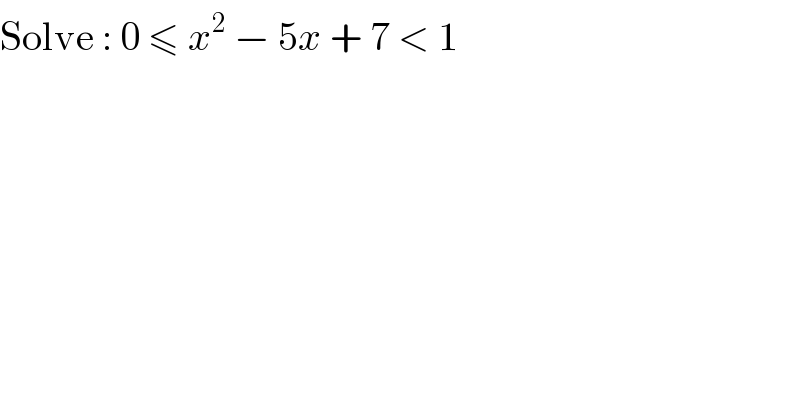
$$\mathrm{Solve}\::\:\mathrm{0}\:\leqslant\:{x}^{\mathrm{2}} \:−\:\mathrm{5}{x}\:+\:\mathrm{7}\:<\:\mathrm{1} \\ $$
Answered by ajfour last updated on 12/Jun/17
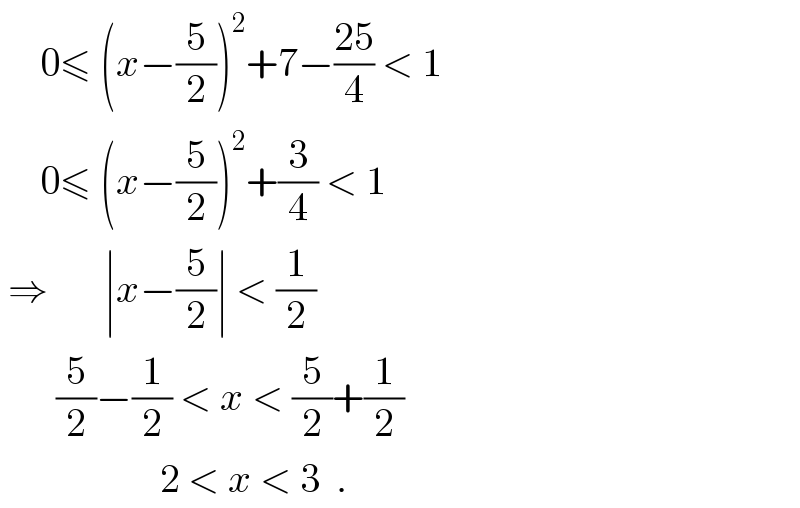
$$\:\:\:\:\:\mathrm{0}\leqslant\:\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{7}−\frac{\mathrm{25}}{\mathrm{4}}\:<\:\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{0}\leqslant\:\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\:<\:\mathrm{1} \\ $$$$\:\Rightarrow\:\:\:\:\:\:\:\mid{x}−\frac{\mathrm{5}}{\mathrm{2}}\mid\:<\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:<\:{x}\:<\:\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:<\:{x}\:<\:\mathrm{3}\:\:. \\ $$
Commented by Tinkutara last updated on 12/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by arnabpapu550@gmail.com last updated on 12/Jun/17
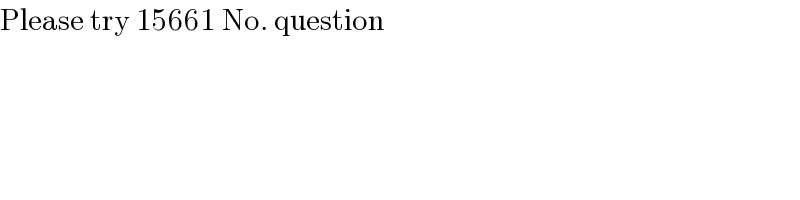
$$\mathrm{Please}\:\mathrm{try}\:\mathrm{15661}\:\mathrm{No}.\:\mathrm{question} \\ $$
