Menu Close

solve-1-0-ln-2-e-x-e-4-x-2-dx-pi-k-e-2-k-2-0-ln-3-x-e-2

Tinku Tara 0 Comments
Pin




Question Number 149673 by mnjuly1970 last updated on 06/Aug/21
solve :: [ 1] 𝛗 := ∫_0 ^( ∞ ) ((ln^( 2) (e x ))/(e^( 4) +x^( 2) )) dx =((Ο€ k)/e^( 2) ) k:= ? [ 2 ] Ξ© := ∫_(0 ) ^( ∞) (( ln^( 3) (x ))/( e^( 2) + x^( 2) )) dx = ?
$$\:\:\:\mathrm{solve}\::: \\ $$$$\left[\:\mathrm{1}\right]\:\:\:\:\boldsymbol{\phi}\::=\:\int_{\mathrm{0}} ^{\:\:\infty\:} \frac{{ln}^{\:\mathrm{2}} \:\left({e}\:{x}\:\right)}{{e}^{\:\mathrm{4}} \:+{x}^{\:\mathrm{2}} }\:{dx}\:=\frac{\pi\:{k}}{{e}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}:=\:? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\left[\:\mathrm{2}\:\right]\:\:\:\Omega\::=\:\int_{\mathrm{0}\:} ^{\:\infty} \:\frac{\:{ln}^{\:\mathrm{3}} \:\left({x}\:\right)}{\:{e}^{\:\mathrm{2}} +\:{x}^{\:\mathrm{2}} }\:{dx}\:=\:? \\ $$
Answered by mathmax by abdo last updated on 06/Aug/21
Ξ¦=∫_0 ^∞ ((ln^2 (ex))/(x^2 +e^4 ))dx changement x=e^2 t give Ξ¦=∫_0 ^∞ ((ln^2 (e^3 t))/(e^4 t^2 +e^4 ))(e^2 dt) =(1/e^2 )∫_0 ^∞ (((3+lnt)^2 )/(t^2 +1))dt β‡’e^2 Ξ¦=∫_0 ^∞ ((ln^2 t+6lnt +9)/(t^2 +1))dt =∫_0 ^∞ ((ln^2 t)/(1+t^2 ))dt+6∫_0 ^∞ ((lnt)/(t^2 +1))dt +9∫_0 ^∞ (dt/(t^2 +1)) ∫_0 ^∞ ((lnt)/(t^2 +1))dt=0(proved) ,∫_0 ^∞ (dt/(t^(2 ) +1))=(Ο€/2) f(a)=∫_0 ^∞ (t^a /(1+t^2 ))dt =∫_0 ^∞ (e^(alnt) /(1+t^2 ))dt β‡’ f^β€² (a)=∫_0 ^∞ ((lnt e^(alnt) )/(1+t^2 ))dt β‡’f^((2)) (a)=∫_0 ^∞ ((t^a ln^2 t)/(t^2 +1))dt β‡’ f^((2)) (0) =∫_0 ^∞ ((ln^2 t)/(t^2 +1))dt changement t^2 =y give t=y^(1/2) f(a)=∫_0 ^∞ (t^(a/2) /(1+y))(1/2)y^((1/2)βˆ’1) dy =(1/2)∫_0 ^∞ (t^(((a+1)/2)βˆ’1) /(1+y))dy =(1/2)Γ—(Ο€/(sin((((a+1)/2))Ο€))) =(Ο€/(2cos(((Ο€a)/2)))) β‡’ f^β€² (a)=(Ο€/2)(βˆ’(((Ο€/2)sin(((Ο€a)/2)))/(cos^2 (((Ο€a)/2)))))=βˆ’(Ο€^2 /4)Γ—((sin(((Ο€a)/2)))/(cos^2 (((Ο€a)/2)))) β‡’ f^((2)) (a)=βˆ’(Ο€^2 /4){(((Ο€/2)cos(((Ο€a)/2))cos^2 (((Ο€a)/2))+2.(Ο€/2)sin(((Ο€a)/2))cos(((Ο€a)/2)))/(cos^4 (((Ο€a)/2))))} =βˆ’(Ο€^3 /8){((cos^2 (((Ο€a)/2))+2sin(((Ο€a)/2)))/(cos^3 (((Ο€a)/2))))} β‡’f^((2)) (0)=βˆ’(Ο€^3 /8) β‡’ e^2 Ξ¦=βˆ’(Ο€^3 /8)+((9Ο€)/2) β‡’Ξ¦=(Ο€/e^2 )(βˆ’(Ο€^2 /8)+(9/2))=((Ο€k)/e^2 ) β‡’k=(9/2)βˆ’(Ο€^2 /8)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{ex}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{e}^{\mathrm{4}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{e}^{\mathrm{2}} \mathrm{t}\:\mathrm{give} \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{3}} \mathrm{t}\right)}{\mathrm{e}^{\mathrm{4}} \mathrm{t}^{\mathrm{2}} \:+\mathrm{e}^{\mathrm{4}} }\left(\mathrm{e}^{\mathrm{2}} \mathrm{dt}\right)\:=\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{3}+\mathrm{lnt}\right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$\Rightarrow\mathrm{e}^{\mathrm{2}} \Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}+\mathrm{6lnt}\:+\mathrm{9}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}+\mathrm{6}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:+\mathrm{9}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}=\mathrm{0}\left(\mathrm{proved}\right)\:\:\:,\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}\:} +\mathrm{1}}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{alnt}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnt}\:\mathrm{e}^{\mathrm{alnt}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}} \mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:\:\mathrm{changement}\:\mathrm{t}^{\mathrm{2}} =\mathrm{y}\:\mathrm{give}\:\mathrm{t}=\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{a}}{\mathrm{2}}} }{\mathrm{1}+\mathrm{y}}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{2}}βˆ’\mathrm{1}} \:\mathrm{dy}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}βˆ’\mathrm{1}} }{\mathrm{1}+\mathrm{y}}\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}Γ—\frac{\pi}{\mathrm{sin}\left(\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}\right)\pi\right)}\:=\frac{\pi}{\mathrm{2cos}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\pi}{\mathrm{2}}\left(βˆ’\frac{\frac{\pi}{\mathrm{2}}\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\right)=βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{4}}Γ—\frac{\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\left\{\frac{\frac{\pi}{\mathrm{2}}\mathrm{cos}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)+\mathrm{2}.\frac{\pi}{\mathrm{2}}\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\right\} \\ $$$$=βˆ’\frac{\pi^{\mathrm{3}} }{\mathrm{8}}\left\{\frac{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)+\mathrm{2sin}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{3}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\right\}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=βˆ’\frac{\pi^{\mathrm{3}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{2}} \Phi=βˆ’\frac{\pi^{\mathrm{3}} }{\mathrm{8}}+\frac{\mathrm{9}\pi}{\mathrm{2}}\:\Rightarrow\Phi=\frac{\pi}{\mathrm{e}^{\mathrm{2}} }\left(βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{2}}\right)=\frac{\pi\mathrm{k}}{\mathrm{e}^{\mathrm{2}} }\:\Rightarrow\mathrm{k}=\frac{\mathrm{9}}{\mathrm{2}}βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by Ar Brandon last updated on 07/Aug/21
Bravo ��
Commented by Tawa11 last updated on 06/Aug/21
great
$$\mathrm{great} \\ $$
Commented by Ar Brandon last updated on 06/Aug/21
Sir, f(a)=(Ο€/(2cos(((Ο€a)/2))))β‡’f β€²(a)=(Ο€^2 /4)βˆ™((sin((Ο€/2)a))/(cos^2 ((Ο€/2)a))) instead of βˆ’(Ο€^2 /4)βˆ™((sin((Ο€/2)a))/(cos^2 ((Ο€/2)a))). Please check ! Line 10 β†’Line 11
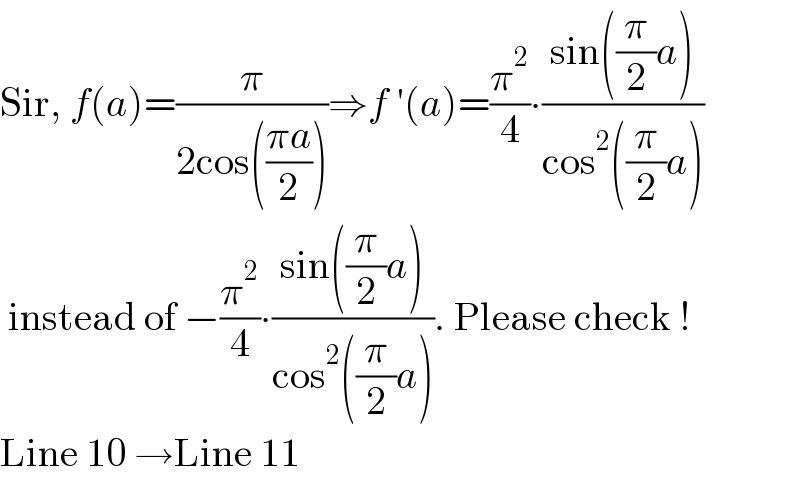
$$\mathrm{Sir},\:{f}\left({a}\right)=\frac{\pi}{\mathrm{2cos}\left(\frac{\pi{a}}{\mathrm{2}}\right)}\Rightarrow{f}\:'\left({a}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\centerdot\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}{a}\right)} \\ $$$$\:\mathrm{instead}\:\mathrm{of}\:βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\centerdot\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}{a}\right)}.\:\mathrm{Please}\:\mathrm{check}\:! \\ $$$$\mathrm{Line}\:\mathrm{10}\:\rightarrow\mathrm{Line}\:\mathrm{11} \\ $$
Commented by mathmax by abdo last updated on 07/Aug/21
sorry f^β€² (a)=(Ο€^2 /4)Γ—((sin(((Ο€a)/2)))/(cos^2 (((Ο€a)/2)))) β‡’ f^((2)) (a)=(Ο€^3 /8)Γ—((cos^2 (((Ο€a)/2))+2sin(((Ο€a)/2)))/(cos^3 (((Ο€a)/2)))) β‡’f^((2)) (0)=(Ο€^3 /8) β‡’ e^2 Ξ¦=(Ο€^3 /8)+((9Ο€)/2) β‡’Ξ¦=(Ο€/e^2 )((Ο€^2 /8)+(9/2)) β‡’k=(Ο€^2 /8)+(9/2)
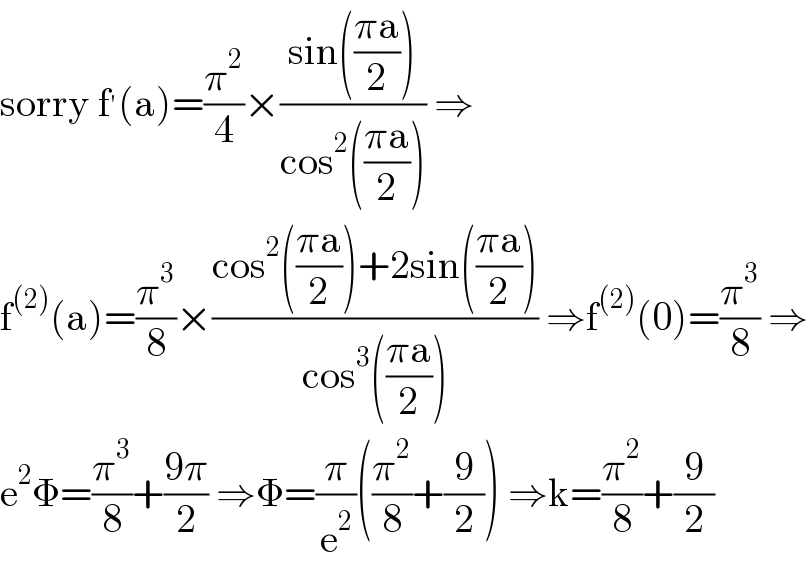
$$\mathrm{sorry}\:\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}Γ—\frac{\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}Γ—\frac{\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)+\mathrm{2sin}\left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}{\mathrm{cos}^{\mathrm{3}} \left(\frac{\pi\mathrm{a}}{\mathrm{2}}\right)}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{2}} \Phi=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}+\frac{\mathrm{9}\pi}{\mathrm{2}}\:\Rightarrow\Phi=\frac{\pi}{\mathrm{e}^{\mathrm{2}} }\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{2}}\right)\:\Rightarrow\mathrm{k}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 07/Aug/21
yes error of sing...!
$$\mathrm{yes}\:\mathrm{error}\:\mathrm{of}\:\mathrm{sing}…! \\ $$
Answered by Ar Brandon last updated on 06/Aug/21
Ο†=∫_0 ^∞ ((ln^2 (ex))/(e^4 +x^2 ))dx=∫_0 ^∞ ((1+2lnx+ln^2 x)/(e^4 +x^2 ))dx =(1/e^2 )∫_0 ^∞ ((1+2ln(e^2 u)+ln^2 (e^2 u))/(1+u^2 ))du =(Ο€/(2e^2 ))+(1/e^2 )∫_0 ^∞ ((4+2lnu+4+4lnu+ln^2 u)/(1+u^2 ))du =(Ο€/(2e^2 ))+((4Ο€)/e^2 )+(1/e^2 )∫_0 ^∞ ((6lnu+ln^2 u)/(1+u^2 ))du =((9Ο€)/(2e^2 ))+(6/e^2 )βˆ™(βˆ‚/βˆ‚Ξ±)∣_(Ξ±=1) ∫_0 ^∞ (u^(Ξ±βˆ’1) /(1+u^2 ))du+(1/e^2 )βˆ™(βˆ‚^2 /βˆ‚Ξ±^2 )∣_(Ξ±=1) ∫_0 ^∞ (u^(Ξ±βˆ’1) /(1+u^2 ))du =((9Ο€)/(2e^2 ))+(3/e^2 )βˆ™(βˆ‚/βˆ‚Ξ±)∣_(Ξ±=1) (Ο€/(sin(((πα)/2))))+(1/(2e^2 ))βˆ™(βˆ‚^2 /βˆ‚Ξ±^2 )∣_(Ξ±=1) (Ο€/(sin(((πα)/2)))) =((9Ο€)/(2e^2 ))βˆ’((3Ο€^2 )/(2e^2 ))∣_(Ξ±=1) cosec(((πα)/2))cot(((πα)/2)) +(Ο€^3 /(8e^2 ))∣_(Ξ±=1) cosec^3 (((πα)/2))+cosec(((πα)/2))cot^2 (((πα)/2)) =((9Ο€)/(2e^2 ))+(Ο€^3 /(8e^2 ))=(Ο€/e^2 )((9/2)+(Ο€^2 /( 8))), k=(9/2)+(Ο€^2 /8)
$$\phi=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}^{\mathrm{2}} \left({ex}\right)}{{e}^{\mathrm{4}} +{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\mathrm{2ln}{x}+\mathrm{ln}^{\mathrm{2}} {x}}{{e}^{\mathrm{4}} +{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\mathrm{2ln}\left({e}^{\mathrm{2}} {u}\right)+\mathrm{ln}^{\mathrm{2}} \left({e}^{\mathrm{2}} {u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{2}{e}^{\mathrm{2}} }+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{4}+\mathrm{2ln}{u}+\mathrm{4}+\mathrm{4ln}{u}+\mathrm{ln}^{\mathrm{2}} {u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{2}{e}^{\mathrm{2}} }+\frac{\mathrm{4}\pi}{{e}^{\mathrm{2}} }+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{6ln}{u}+\mathrm{ln}^{\mathrm{2}} {u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:=\frac{\mathrm{9}\pi}{\mathrm{2}{e}^{\mathrm{2}} }+\frac{\mathrm{6}}{{e}^{\mathrm{2}} }\centerdot\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alphaβˆ’\mathrm{1}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du}+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\centerdot\frac{\partial^{\mathrm{2}} }{\partial\alpha^{\mathrm{2}} }\mid_{\alpha=\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alphaβˆ’\mathrm{1}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:=\frac{\mathrm{9}\pi}{\mathrm{2}{e}^{\mathrm{2}} }+\frac{\mathrm{3}}{{e}^{\mathrm{2}} }\centerdot\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \frac{\pi}{\mathrm{sin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)}+\frac{\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}} }\centerdot\frac{\partial^{\mathrm{2}} }{\partial\alpha^{\mathrm{2}} }\mid_{\alpha=\mathrm{1}} \frac{\pi}{\mathrm{sin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\frac{\mathrm{9}\pi}{\mathrm{2}{e}^{\mathrm{2}} }βˆ’\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{2}{e}^{\mathrm{2}} }\mid_{\alpha=\mathrm{1}} \mathrm{cosec}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\mathrm{cot}\left(\frac{\pi\alpha}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:+\frac{\pi^{\mathrm{3}} }{\mathrm{8}{e}^{\mathrm{2}} }\mid_{\alpha=\mathrm{1}} \mathrm{cosec}^{\mathrm{3}} \left(\frac{\pi\alpha}{\mathrm{2}}\right)+\mathrm{cosec}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\mathrm{cot}^{\mathrm{2}} \left(\frac{\pi\alpha}{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\mathrm{9}\pi}{\mathrm{2}{e}^{\mathrm{2}} }+\frac{\pi^{\mathrm{3}} }{\mathrm{8}{e}^{\mathrm{2}} }=\frac{\pi}{{e}^{\mathrm{2}} }\left(\frac{\mathrm{9}}{\mathrm{2}}+\frac{\pi^{\mathrm{2}} }{\:\mathrm{8}}\right),\:{k}=\frac{\mathrm{9}}{\mathrm{2}}+\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by Ar Brandon last updated on 06/Aug/21
It was a pleasure, Sir ��
Commented by mnjuly1970 last updated on 06/Aug/21
very nice mr brandon..
$${very}\:{nice}\:{mr}\:{brandon}.. \\ $$
Answered by Ar Brandon last updated on 06/Aug/21
Ξ©=∫_0 ^∞ ((ln^3 x)/(e^2 +x^2 ))dx=(1/e)∫_0 ^∞ ((ln^3 (eu))/(1+u^2 ))du =(1/e)∫_0 ^∞ ((1+3lnu+3ln^2 u+ln^3 u)/(1+u^2 ))du =(Ο€/(2e))+((3Ο€^3 )/(8e))+(1/e)∫_0 ^∞ ((ln^3 u)/(1+u^2 ))du =(((4+3Ο€^2 )Ο€)/(8e))+(1/e)βˆ™(βˆ‚^3 /βˆ‚Ξ±^3 )∣_(Ξ±=1) ∫_0 ^∞ (u^(Ξ±βˆ’1) /(1+u^2 ))du =(((4+3Ο€^2 )Ο€)/(8e))+(1/e)βˆ™(βˆ‚^3 /βˆ‚Ξ±^3 )∣_(Ξ±=1) (Ο€/(sin(((πα)/2)))) =(((4+3Ο€^2 )Ο€)/(8e))βˆ’(Ο€/(8e))∣_(Ξ±=1) (((3Ο€)/2)cosec^2 (((πα)/2))cosec(((πα)/2))cot(((πα)/2)) +Ο€(cosec^3 (((πα)/2))cot(((πα)/2))+(1/2)cosec(((πα)/2))cot^3 (((πα)/2))) =(((4+3Ο€^2 )Ο€)/(8e))
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}^{\mathrm{3}} {x}}{{e}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{{e}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}^{\mathrm{3}} \left({eu}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{{e}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\mathrm{3ln}{u}+\mathrm{3ln}^{\mathrm{2}} {u}+\mathrm{ln}^{\mathrm{3}} {u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2}{e}}+\frac{\mathrm{3}\pi^{\mathrm{3}} }{\mathrm{8}{e}}+\frac{\mathrm{1}}{{e}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}^{\mathrm{3}} {u}}{\mathrm{1}+{u}^{\mathrm{2}} }\mathrm{d}{u} \\ $$$$\:\:\:\:=\frac{\left(\mathrm{4}+\mathrm{3}\pi^{\mathrm{2}} \right)\pi}{\mathrm{8}{e}}+\frac{\mathrm{1}}{{e}}\centerdot\frac{\partial^{\mathrm{3}} }{\partial\alpha^{\mathrm{3}} }\mid_{\alpha=\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alphaβˆ’\mathrm{1}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:\:\:=\frac{\left(\mathrm{4}+\mathrm{3}\pi^{\mathrm{2}} \right)\pi}{\mathrm{8}{e}}+\frac{\mathrm{1}}{{e}}\centerdot\frac{\partial^{\mathrm{3}} }{\partial\alpha^{\mathrm{3}} }\mid_{\alpha=\mathrm{1}} \frac{\pi}{\mathrm{sin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:=\frac{\left(\mathrm{4}+\mathrm{3}\pi^{\mathrm{2}} \right)\pi}{\mathrm{8}{e}}βˆ’\frac{\pi}{\mathrm{8}{e}}\mid_{\alpha=\mathrm{1}} \left(\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{cosec}^{\mathrm{2}} \left(\frac{\pi\alpha}{\mathrm{2}}\right)\mathrm{cosec}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\mathrm{cot}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:+\pi\left(\mathrm{cosec}^{\mathrm{3}} \left(\frac{\pi\alpha}{\mathrm{2}}\right)\mathrm{cot}\left(\frac{\pi\alpha}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosec}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\mathrm{cot}^{\mathrm{3}} \left(\frac{\pi\alpha}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:=\frac{\left(\mathrm{4}+\mathrm{3}\pi^{\mathrm{2}} \right)\pi}{\mathrm{8}{e}} \\ $$
Commented by mnjuly1970 last updated on 06/Aug/21
bravo mr brandon...
$${bravo}\:{mr}\:{brandon}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *