Menu Close

solve-1-2-2h-3-2-h-1-

Tinku Tara 0 Comments
Pin




Question Number 116610 by moh175 last updated on 05/Oct/20
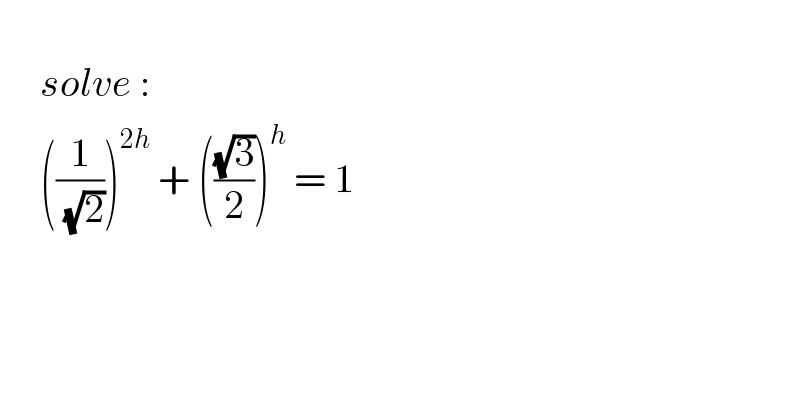
solve : ((1/( (√2))))^(2h) + (((√3)/2))^h = 1
$$ \\ $$$$\:\:\:\:\:{solve}\:: \\ $$$$\:\:\:\:\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{h}} \:+\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{{h}} \:=\:\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 05/Oct/20
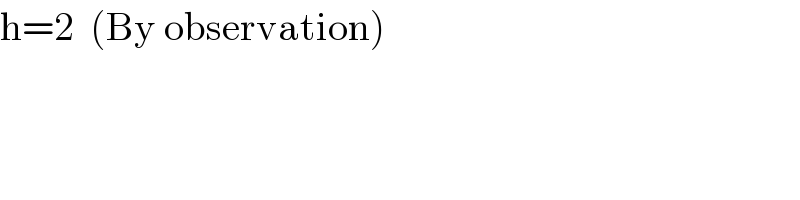
h=2 (By observation)
$$\mathrm{h}=\mathrm{2}\:\:\left(\mathrm{By}\:\mathrm{observation}\right) \\ $$
Answered by 1549442205PVT last updated on 05/Oct/20
We have ((1/( (√2))))^(2h) + (((√3)/2))^h = 1⇔((1/2))^h +(((√3)/2))^h =1(1) It is easy to see that h=2 satisfy the equation since ((1/2))^2 +(((√3)/2))^2 =(1/4)+(3/4)=1 We note that 0<(1/2)<((√3)/2)<1.Hence ((1/2))^x and (((√3)/2))^x both are decreasing functions on (0;+∞).Therefore i)If h>2 then ((1/2))^h +(((√3)/2))^h <((1/2))^2 +(((√3)/2))^2 =1 ii)If h<2 then then ((1/2))^h +(((√3)/2))^h >((1/2))^2 +(((√3)/2))^2 =1 That shows h=2 is unique root of given equation
$$\mathrm{We}\:\mathrm{have} \\ $$$$\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{h}} \:+\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{{h}} \:=\:\mathrm{1}\Leftrightarrow\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{h}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{h}} =\mathrm{1}\left(\mathrm{1}\right) \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{h}=\mathrm{2}\:\mathrm{satisfy}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{since}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{1} \\ $$$$\mathrm{We}\:\mathrm{note}\:\mathrm{that}\:\mathrm{0}<\frac{\mathrm{1}}{\mathrm{2}}<\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}<\mathrm{1}.\mathrm{Hence} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{x}} \mathrm{and}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{x}} \mathrm{both}\:\mathrm{are}\:\mathrm{decreasing}\:\mathrm{functions} \\ $$$$\mathrm{on}\:\left(\mathrm{0};+\infty\right).\mathrm{Therefore} \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\mathrm{h}>\mathrm{2}\:\mathrm{then}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{h}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{h}} <\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{h}<\mathrm{2}\:\mathrm{then} \\ $$$$\:\mathrm{then}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{h}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{h}} >\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{That}\:\mathrm{shows}\:\mathrm{h}=\mathrm{2}\:\mathrm{is}\:\mathrm{unique}\:\mathrm{root}\:\mathrm{of} \\ $$$$\mathrm{given}\:\mathrm{equation} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *