Question Number 31017 by 78987 last updated on 02/Mar/18
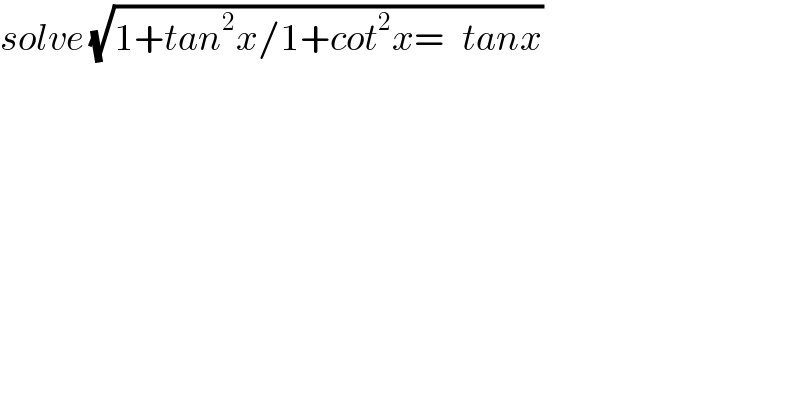
$${solve}\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {x}/\mathrm{1}+{cot}^{\mathrm{2}} {x}=\:\:\:{tanx}} \\ $$
Answered by iv@0uja last updated on 02/Mar/18
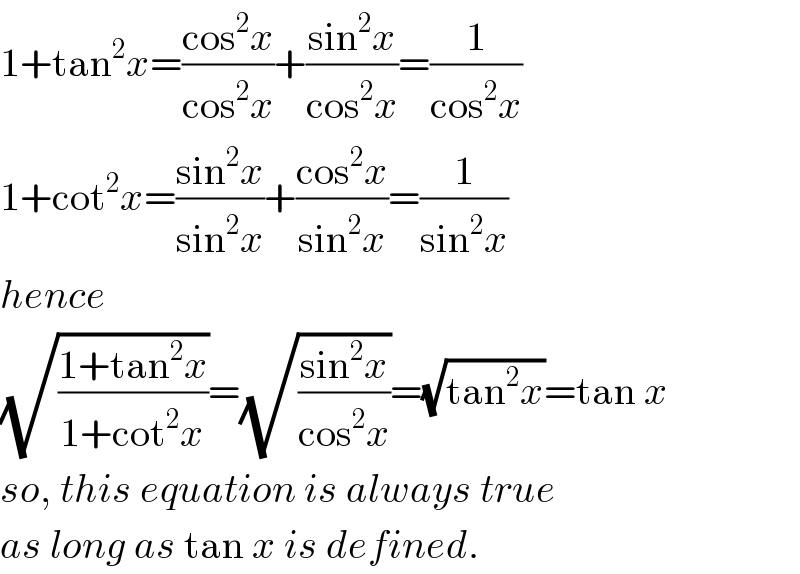
$$\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}=\frac{\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{cos}^{\mathrm{2}} {x}}+\frac{\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{cos}^{\mathrm{2}} {x}}=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} {x}} \\ $$$$\mathrm{1}+\mathrm{cot}^{\mathrm{2}} {x}=\frac{\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{sin}^{\mathrm{2}} {x}}+\frac{\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{sin}^{\mathrm{2}} {x}}=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} {x}} \\ $$$${hence} \\ $$$$\sqrt{\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{cot}^{\mathrm{2}} {x}}}=\sqrt{\frac{\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{cos}^{\mathrm{2}} {x}}}=\sqrt{\mathrm{tan}^{\mathrm{2}} {x}}=\mathrm{tan}\:{x} \\ $$$${so},\:{this}\:{equation}\:{is}\:{always}\:{true} \\ $$$${as}\:{long}\:{as}\:\mathrm{tan}\:{x}\:{is}\:{defined}. \\ $$
