Question Number 92346 by M±th+et+s last updated on 06/May/20
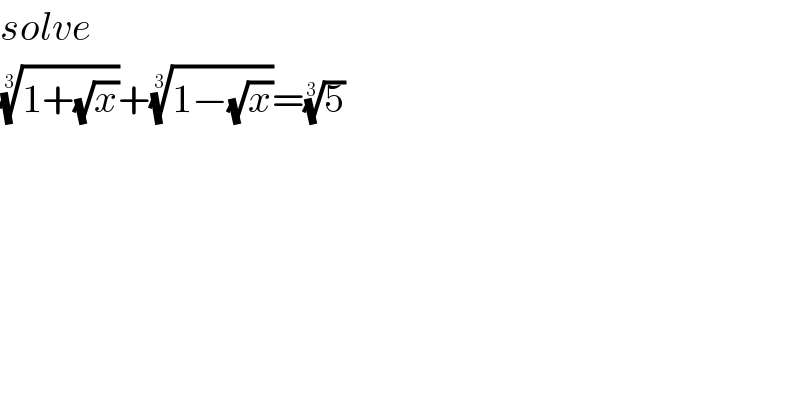
$${solve} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{{x}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\sqrt{{x}}}=\sqrt[{\mathrm{3}}]{\mathrm{5}} \\ $$
Commented by jagoll last updated on 06/May/20

$$\mathrm{x}\:\approx\:.\mathrm{79999999722742} \\ $$
Commented by M±th+et+s last updated on 06/May/20
correct ����
Commented by mr W last updated on 06/May/20

$${x}=\mathrm{0}.\mathrm{8}\:{exactly} \\ $$
Answered by mr W last updated on 06/May/20
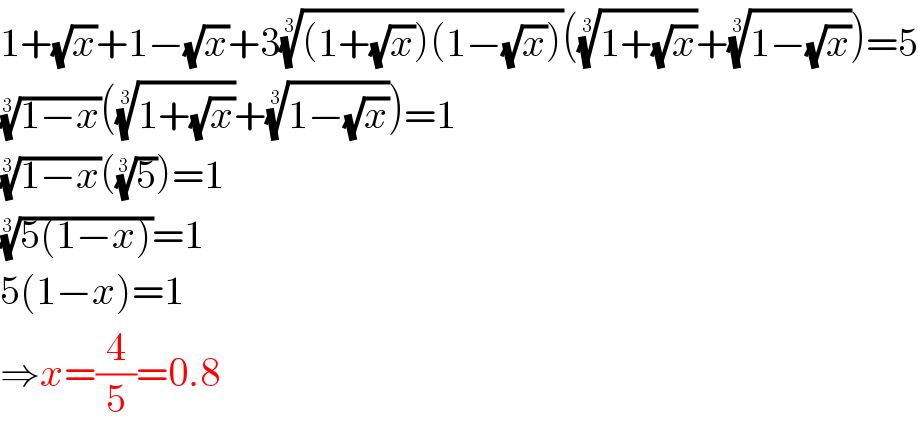
$$\mathrm{1}+\sqrt{{x}}+\mathrm{1}−\sqrt{{x}}+\mathrm{3}\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\sqrt{{x}}\right)\left(\mathrm{1}−\sqrt{{x}}\right)}\left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{{x}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\sqrt{{x}}}\right)=\mathrm{5} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}}\left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{{x}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−\sqrt{{x}}}\right)=\mathrm{1} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}}\left(\sqrt[{\mathrm{3}}]{\mathrm{5}}\right)=\mathrm{1} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{5}\left(\mathrm{1}−{x}\right)}=\mathrm{1} \\ $$$$\mathrm{5}\left(\mathrm{1}−{x}\right)=\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{0}.\mathrm{8} \\ $$
Commented by M±th+et+s last updated on 06/May/20

$${thank}\:{you}\:{sir} \\ $$
Answered by behi83417@gmail.com last updated on 06/May/20
![1+(√x)=a^3 ,1−(√x)=b^3 ⇒ { ((a^3 +b^3 =2)),((a+b=(5)^(1/3) )) :}⇒(a+b)[(a+b)^2 −3ab]=2 ⇒(5)^(1/3) [(5^2 )^(1/3) −3ab]=2⇒ab=(1/3)[(5^2 )^(1/3) −(2/( (5)^(1/3) ))] ⇒ab=(1/( (5)^(1/3) ))⇒a^3 b^3 =(1/5) ⇒z^2 −2z+(1/5)=0⇒z=[a^3 ∨b^3 ]=1±(√(1^2 −(1/5)))=(((√5)±2)/( (√5))) ⇒1+(√x)=(((√5)±2)/( (√5)))⇒(√x)=(((√5)±2−(√5))/( (√5)))=((±2)/( (√5))) ⇒x=(4/5)=0.8 ⇒1−(√x)=(((√5)±2)/( (√5)))⇒(√x)=(((√5)−(√5)∓2)/( (√5)))=((∓2)/( (√5))) ⇒x=(4/5)=0.8 .■](https://www.tinkutara.com/question/Q92376.png)
$$\mathrm{1}+\sqrt{\mathrm{x}}=\mathrm{a}^{\mathrm{3}} ,\mathrm{1}−\sqrt{\mathrm{x}}=\mathrm{b}^{\mathrm{3}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\mathrm{2}}\\{\mathrm{a}+\mathrm{b}=\sqrt[{\mathrm{3}}]{\mathrm{5}}}\end{cases}\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)\left[\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} −\mathrm{3ab}\right]=\mathrm{2} \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{5}}\left[\sqrt[{\mathrm{3}}]{\mathrm{5}^{\mathrm{2}} }−\mathrm{3ab}\right]=\mathrm{2}\Rightarrow\mathrm{ab}=\frac{\mathrm{1}}{\mathrm{3}}\left[\sqrt[{\mathrm{3}}]{\mathrm{5}^{\mathrm{2}} }−\frac{\mathrm{2}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}}}\right] \\ $$$$\Rightarrow\mathrm{ab}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}}}\Rightarrow\mathrm{a}^{\mathrm{3}} \mathrm{b}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{z}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{z}}+\frac{\mathrm{1}}{\mathrm{5}}=\mathrm{0}\Rightarrow\boldsymbol{\mathrm{z}}=\left[\mathrm{a}^{\mathrm{3}} \vee\mathrm{b}^{\mathrm{3}} \right]=\mathrm{1}\pm\sqrt{\mathrm{1}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{5}}}=\frac{\sqrt{\mathrm{5}}\pm\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\mathrm{1}+\sqrt{\mathrm{x}}=\frac{\sqrt{\mathrm{5}}\pm\mathrm{2}}{\:\sqrt{\mathrm{5}}}\Rightarrow\sqrt{\mathrm{x}}=\frac{\sqrt{\mathrm{5}}\pm\mathrm{2}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}}=\frac{\pm\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{0}.\mathrm{8} \\ $$$$\Rightarrow\mathrm{1}−\sqrt{\mathrm{x}}=\frac{\sqrt{\mathrm{5}}\pm\mathrm{2}}{\:\sqrt{\mathrm{5}}}\Rightarrow\sqrt{\mathrm{x}}=\frac{\sqrt{\mathrm{5}}−\sqrt{\mathrm{5}}\mp\mathrm{2}}{\:\sqrt{\mathrm{5}}}=\frac{\mp\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{0}.\mathrm{8}\:\:.\blacksquare \\ $$
Commented by M±th+et+s last updated on 06/May/20

$${cool}. \\ $$$${thank}\:{you}\:{sir} \\ $$
Answered by john santu last updated on 06/May/20
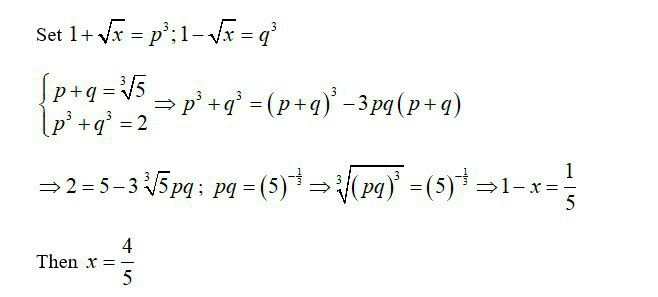
Commented by M±th+et+s last updated on 06/May/20

$${thank}\:{you} \\ $$
Commented by jagoll last updated on 06/May/20
jooss ������
