Menu Close

solve-1-x-1-y-1-z-3-4-with-x-y-z-N-

Tinku Tara 0 Comments
Pin




Question Number 118322 by mr W last updated on 16/Oct/20
solve (1/x)+(1/y)+(1/z)=(3/4) with x,y,z∈N
$${solve} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${with}\:{x},{y},{z}\in\mathbb{N} \\ $$
Commented by malwaan last updated on 17/Oct/20
((yz+xz+xy)/(xyz)) = (3/4) (x≠0;y≠0;z≠0) 1) x = y = z ⇒((3x^2 )/x^3 ) = (3/4)⇒(3/x) = (3/4) ⇒x=y=z=4 2) if x=1⇒(1/y) + (1/z)=−(1/4){wrong} so x>1 ; y>1 ;z>1 3) x=2⇒(1/y) + (1/z) = (1/4) ⇒y=8 ; z=8 4) x=3⇒(1/y) + (1/z) = (5/(12)) ((y+z)/(yz)) = (5/(12)){no solutions} so x≠3 ; y≠3 ; z≠3
$$\frac{{yz}+{xz}+{xy}}{{xyz}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:\left({x}\neq\mathrm{0};{y}\neq\mathrm{0};{z}\neq\mathrm{0}\right) \\ $$$$\left.\mathrm{1}\right)\:{x}\:=\:{y}\:=\:{z} \\ $$$$\Rightarrow\frac{\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow\frac{\mathrm{3}}{{x}}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{x}={y}={z}=\mathrm{4} \\ $$$$\left.\mathrm{2}\right)\:\:{if}\:{x}=\mathrm{1}\Rightarrow\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{z}}=−\frac{\mathrm{1}}{\mathrm{4}}\left\{{wrong}\right\} \\ $$$${so}\:{x}>\mathrm{1}\:;\:{y}>\mathrm{1}\:;{z}>\mathrm{1} \\ $$$$\left.\mathrm{3}\right)\:{x}=\mathrm{2}\Rightarrow\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{z}}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{y}=\mathrm{8}\:;\:{z}=\mathrm{8} \\ $$$$\left.\mathrm{4}\right)\:{x}=\mathrm{3}\Rightarrow\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{z}}\:=\:\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\frac{{y}+{z}}{{yz}}\:=\:\frac{\mathrm{5}}{\mathrm{12}}\left\{{no}\:{solutions}\right\} \\ $$$${so}\:{x}\neq\mathrm{3}\:;\:{y}\neq\mathrm{3}\:;\:{z}\neq\mathrm{3} \\ $$
Commented by MJS_new last updated on 17/Oct/20
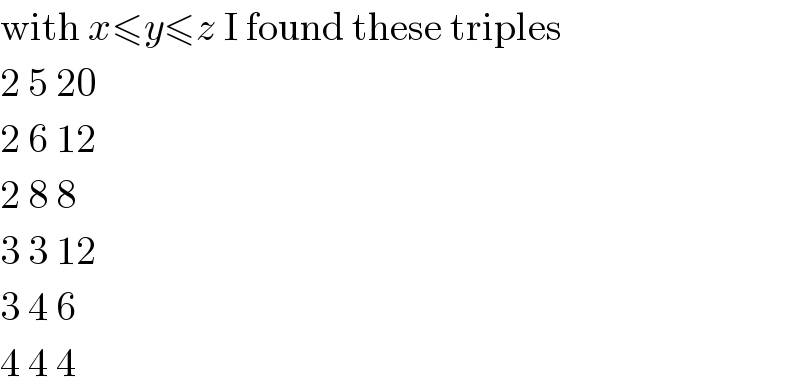
with x≤y≤z I found these triples 2 5 20 2 6 12 2 8 8 3 3 12 3 4 6 4 4 4
$$\mathrm{with}\:{x}\leqslant{y}\leqslant{z}\:\mathrm{I}\:\mathrm{found}\:\mathrm{these}\:\mathrm{triples} \\ $$$$\mathrm{2}\:\mathrm{5}\:\mathrm{20} \\ $$$$\mathrm{2}\:\mathrm{6}\:\mathrm{12} \\ $$$$\mathrm{2}\:\mathrm{8}\:\mathrm{8} \\ $$$$\mathrm{3}\:\mathrm{3}\:\mathrm{12} \\ $$$$\mathrm{3}\:\mathrm{4}\:\mathrm{6} \\ $$$$\mathrm{4}\:\mathrm{4}\:\mathrm{4} \\ $$
Answered by TANMAY PANACEA last updated on 16/Oct/20
x=y=z=4 x=2 y=z=8 it is not solution..by trial
$${x}={y}={z}=\mathrm{4} \\ $$$${x}=\mathrm{2}\:\:{y}={z}=\mathrm{8} \\ $$$${it}\:{is}\:{not}\:{solution}..{by}\:{trial} \\ $$
Answered by 1549442205PVT last updated on 17/Oct/20
(1/x)+(1/y)+(1/z)=(3/4)(1) Since x,y,z have equal role in the equality ,WLOG we can assume that x≥y≥z>1 Then (1/x)≤(1/y)≤(1/z)<1.Hence (3/4)=(1/x)+(1/y)+(1/z)≤(3/z)⇒z≤4 i)For z=4 substituting into (1) we get (2/y)≥(1/x)+(1/y)=(1/2)(2)⇒y≤4⇒y∈{1,2,3,4} •For y=4 substituting into(2)we get (1/x)=(1/2)−(1/4)=(1/4)⇒x=4 •For y=3 substituting into(2)we get (1/x)=(1/2)−(1/3)=(1/6)⇒x=6 •For y∈{1,2}substituting into(2)we get L.H.S (2)>(1/2)⇒has no roots ii)For z=3 substituting into(1)we get (2/y)≥(1/x)+(1/y)=(3/4)−(1/3)=(5/(12))(3)⇒5y≤24. Since y∈N⇒y∈{1,2,3,4} •For y=4 substituting into(3)we get (1/x)=(5/(12))−(1/4)=(2/(12))=(1/6)⇒x=6 •For y=3 substituting into(3)we get (1/x)=(5/(12))−(1/3)=(1/(12))⇒x=12 •For y∈{1,2}substituting into(3)we get L.H.S (3)>(5/(12))⇒has no roots iii)For z=2substituting into(1)we get (2/y)≥(1/x)+(1/y)=(3/4)−(1/2)=(1/4)(4)⇒y≤8 •For y=8 substituting into(4)we get (1/x)=(1/4)−(1/8)=(1/8)⇒x=8 •For y=7 substituting into(4)we get (1/x)=(1/4)−(1/7)=(3/(28))⇒3x=28⇒x∉N •For y=6 substituting into(4)we get (1/x)=(1/4)−(1/6)=(1/(12))⇒x=12 •For y=5 substituting into(4)we get (1/x)=(1/4)−(1/5)=(1/(20))⇒x=20 •For y∈{1,2,3,4} substituting into(4) we get L.H.S(4)>(1/4)⇒has no roots Combining three above cases we obtain 6 roots are: (x,y,z)∈{(4,4,4),(6,4,3),(12,3,3) (8,8,2),(12,6,2),(20,5,2)}(∗) Consequently,the equation (1/x)+(1/y)+(1/z)=(3/4) has 3.3!+2.((3!)/2)+1=25 roots (x,y,z).They are elements of (∗) and all their permutation
$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}\right) \\ $$$$\mathrm{Since}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{have}\:\mathrm{equal}\:\mathrm{role}\:\mathrm{in}\:\mathrm{the}\:\mathrm{equality} \\ $$$$,\mathrm{WLOG}\:\mathrm{we}\:\mathrm{can}\:\mathrm{assume}\:\mathrm{that}\:\mathrm{x}\geqslant\mathrm{y}\geqslant\mathrm{z}>\mathrm{1} \\ $$$$\mathrm{Then}\:\frac{\mathrm{1}}{\mathrm{x}}\leqslant\frac{\mathrm{1}}{\mathrm{y}}\leqslant\frac{\mathrm{1}}{\mathrm{z}}<\mathrm{1}.\mathrm{Hence} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\leqslant\frac{\mathrm{3}}{\mathrm{z}}\Rightarrow\mathrm{z}\leqslant\mathrm{4} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{z}=\mathrm{4}\:\mathrm{substituting}\:\mathrm{into}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{2}}{\mathrm{y}}\geqslant\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\right)\Rightarrow\mathrm{y}\leqslant\mathrm{4}\Rightarrow\mathrm{y}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{4}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{x}=\mathrm{4} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{3}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{6}}\Rightarrow\mathrm{x}=\mathrm{6} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}\in\left\{\mathrm{1},\mathrm{2}\right\}\mathrm{substituting}\:\mathrm{into}\left(\mathrm{2}\right)\mathrm{we}\: \\ $$$$\mathrm{get}\:\mathrm{L}.\mathrm{H}.\mathrm{S}\:\left(\mathrm{2}\right)>\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\left.\mathrm{ii}\right)\mathrm{For}\:\mathrm{z}=\mathrm{3}\:\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{2}}{\mathrm{y}}\geqslant\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{12}}\left(\mathrm{3}\right)\Rightarrow\mathrm{5y}\leqslant\mathrm{24}. \\ $$$$\mathrm{Since}\:\mathrm{y}\in\mathrm{N}\Rightarrow\mathrm{y}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{4}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{5}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{6}}\Rightarrow\mathrm{x}=\mathrm{6} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{3}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{5}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{12}}\Rightarrow\mathrm{x}=\mathrm{12} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}\in\left\{\mathrm{1},\mathrm{2}\right\}\mathrm{substituting}\:\mathrm{into}\left(\mathrm{3}\right)\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{L}.\mathrm{H}.\mathrm{S}\:\left(\mathrm{3}\right)>\frac{\mathrm{5}}{\mathrm{12}}\Rightarrow\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\left.\mathrm{iii}\right)\mathrm{For}\:\mathrm{z}=\mathrm{2substituting}\:\mathrm{into}\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{2}}{\mathrm{y}}\geqslant\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}\right)\Rightarrow\mathrm{y}\leqslant\mathrm{8} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{8}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{8}}\Rightarrow\mathrm{x}=\mathrm{8} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{7}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{3}}{\mathrm{28}}\Rightarrow\mathrm{3x}=\mathrm{28}\Rightarrow\mathrm{x}\notin\mathrm{N}\: \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{6}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{12}}\Rightarrow\mathrm{x}=\mathrm{12} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}=\mathrm{5}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{20}}\Rightarrow\mathrm{x}=\mathrm{20} \\ $$$$\bullet\mathrm{For}\:\mathrm{y}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\}\:\mathrm{substituting}\:\mathrm{into}\left(\mathrm{4}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{L}.\mathrm{H}.\mathrm{S}\left(\mathrm{4}\right)>\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\mathrm{Combining}\:\mathrm{three}\:\mathrm{above}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{obtain} \\ $$$$\mathrm{6}\:\:\mathrm{roots}\:\mathrm{are}: \\ $$$$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)\in\left\{\left(\mathrm{4},\mathrm{4},\mathrm{4}\right),\left(\mathrm{6},\mathrm{4},\mathrm{3}\right),\left(\mathrm{12},\mathrm{3},\mathrm{3}\right)\right. \\ $$$$\left.\left(\mathrm{8},\mathrm{8},\mathrm{2}\right),\left(\mathrm{12},\mathrm{6},\mathrm{2}\right),\left(\mathrm{20},\mathrm{5},\mathrm{2}\right)\right\}\left(\ast\right) \\ $$$$\boldsymbol{\mathrm{Consequently}},\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{equation}}\:\: \\ $$$$\frac{\mathrm{1}}{\boldsymbol{{x}}}+\frac{\mathrm{1}}{\boldsymbol{{y}}}+\frac{\mathrm{1}}{\boldsymbol{{z}}}=\frac{\mathrm{3}}{\mathrm{4}}\:\boldsymbol{\mathrm{has}}\:\mathrm{3}.\mathrm{3}!+\mathrm{2}.\frac{\mathrm{3}!}{\mathrm{2}}+\mathrm{1}=\mathrm{25}\: \\ $$$$\boldsymbol{\mathrm{roots}}\:\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}}\right).\boldsymbol{\mathrm{They}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{elements}}\:\boldsymbol{\mathrm{of}}\:\:\left(\ast\right) \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{their}}\:\boldsymbol{\mathrm{permutation}} \\ $$
Commented by mr W last updated on 17/Oct/20
thank you all sirs!
$${thank}\:{you}\:{all}\:{sirs}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *