Question Number 103412 by abdomsup last updated on 14/Jul/20

$${solve}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} {y}^{''} \:+\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:+\mathrm{2}=\mathrm{0} \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
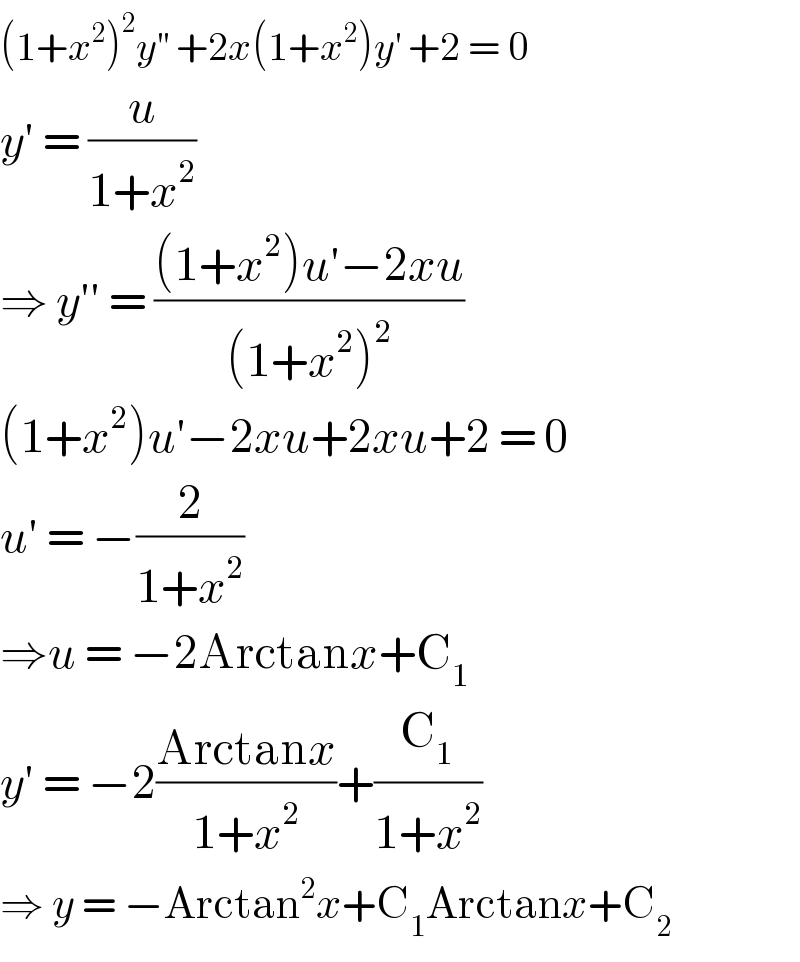
$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} {y}^{''} \:+\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:+\mathrm{2}\:=\:\mathrm{0} \\ $$$${y}'\:=\:\frac{{u}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{y}''\:=\:\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right){u}'−\mathrm{2}{xu}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){u}'−\mathrm{2}{xu}+\mathrm{2}{xu}+\mathrm{2}\:=\:\mathrm{0} \\ $$$${u}'\:=\:−\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{u}\:=\:−\mathrm{2Arctan}{x}+\mathrm{C}_{\mathrm{1}} \\ $$$${y}'\:=\:−\mathrm{2}\frac{\mathrm{Arctan}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{\mathrm{C}_{\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{y}\:=\:−\mathrm{Arctan}^{\mathrm{2}} {x}+\mathrm{C}_{\mathrm{1}} \mathrm{Arctan}{x}+\mathrm{C}_{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 15/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
