Menu Close

solve-1-x-2-dy-dx-xy-xy-2-

Tinku Tara 0 Comments
Pin




Question Number 97001 by bemath last updated on 06/Jun/20
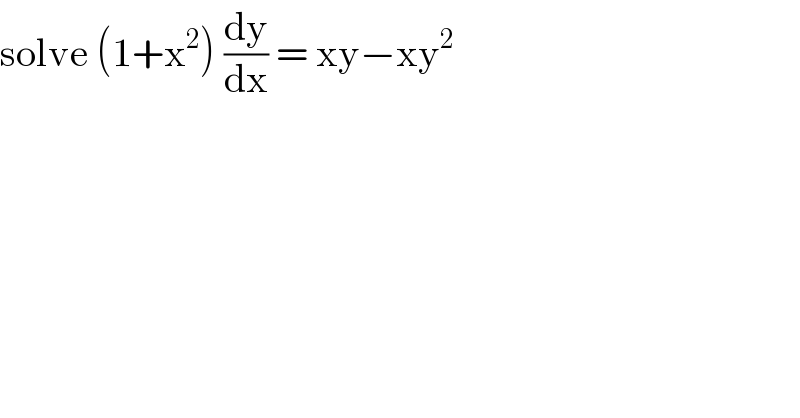
solve (1+x^2 ) (dy/dx) = xy−xy^2
$$\mathrm{solve}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{xy}−\mathrm{xy}^{\mathrm{2}} \\ $$
Commented by bobhans last updated on 06/Jun/20
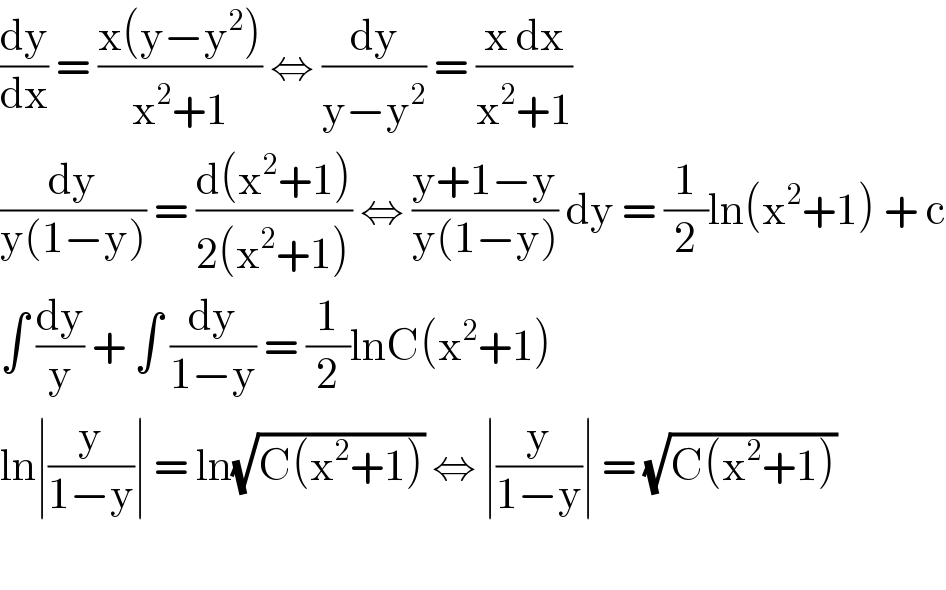
(dy/dx) = ((x(y−y^2 ))/(x^2 +1)) ⇔ (dy/(y−y^2 )) = ((x dx)/(x^2 +1)) (dy/(y(1−y))) = ((d(x^2 +1))/(2(x^2 +1))) ⇔ ((y+1−y)/(y(1−y))) dy = (1/2)ln(x^2 +1) + c ∫ (dy/y) + ∫ (dy/(1−y)) = (1/2)lnC(x^2 +1) ln∣(y/(1−y))∣ = ln(√(C(x^2 +1))) ⇔ ∣(y/(1−y))∣ = (√(C(x^2 +1)))
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}\left(\mathrm{y}−\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\Leftrightarrow\:\frac{\mathrm{dy}}{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }\:=\:\frac{\mathrm{x}\:\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{y}\left(\mathrm{1}−\mathrm{y}\right)}\:=\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\:\Leftrightarrow\:\frac{\mathrm{y}+\mathrm{1}−\mathrm{y}}{\mathrm{y}\left(\mathrm{1}−\mathrm{y}\right)}\:\mathrm{dy}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\:+\:\mathrm{c} \\ $$$$\int\:\frac{\mathrm{dy}}{\mathrm{y}}\:+\:\int\:\frac{\mathrm{dy}}{\mathrm{1}−\mathrm{y}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lnC}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\mathrm{ln}\mid\frac{\mathrm{y}}{\mathrm{1}−\mathrm{y}}\mid\:=\:\mathrm{ln}\sqrt{\mathrm{C}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\:\Leftrightarrow\:\mid\frac{\mathrm{y}}{\mathrm{1}−\mathrm{y}}\mid\:=\:\sqrt{\mathrm{C}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$ \\ $$
Commented by bemath last updated on 06/Jun/20
thanks
$$\mathrm{thanks} \\ $$
Answered by mathmax by abdo last updated on 06/Jun/20
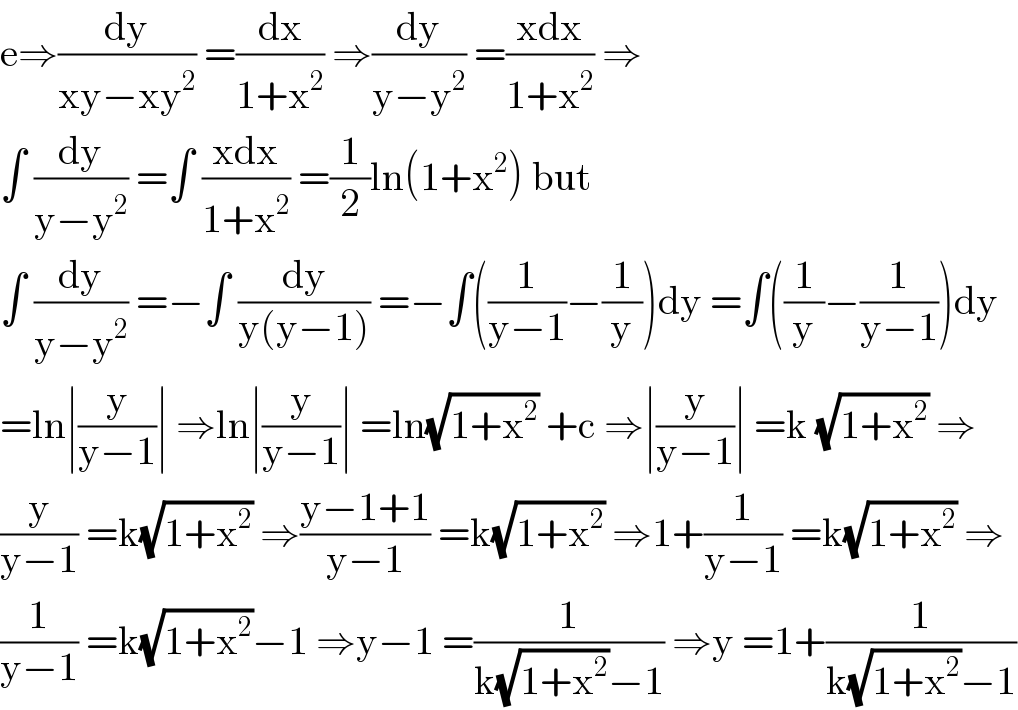
e⇒(dy/(xy−xy^2 )) =(dx/(1+x^2 )) ⇒(dy/(y−y^2 )) =((xdx)/(1+x^2 )) ⇒ ∫ (dy/(y−y^2 )) =∫ ((xdx)/(1+x^2 )) =(1/2)ln(1+x^2 ) but ∫ (dy/(y−y^2 )) =−∫ (dy/(y(y−1))) =−∫((1/(y−1))−(1/y))dy =∫((1/y)−(1/(y−1)))dy =ln∣(y/(y−1))∣ ⇒ln∣(y/(y−1))∣ =ln(√(1+x^2 )) +c ⇒∣(y/(y−1))∣ =k (√(1+x^2 )) ⇒ (y/(y−1)) =k(√(1+x^2 )) ⇒((y−1+1)/(y−1)) =k(√(1+x^2 )) ⇒1+(1/(y−1)) =k(√(1+x^2 )) ⇒ (1/(y−1)) =k(√(1+x^2 ))−1 ⇒y−1 =(1/(k(√(1+x^2 ))−1)) ⇒y =1+(1/(k(√(1+x^2 ))−1))
$$\mathrm{e}\Rightarrow\frac{\mathrm{dy}}{\mathrm{xy}−\mathrm{xy}^{\mathrm{2}} }\:=\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }\:=\frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\frac{\mathrm{dy}}{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }\:=\int\:\frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{but} \\ $$$$\int\:\frac{\mathrm{dy}}{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }\:=−\int\:\frac{\mathrm{dy}}{\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)}\:=−\int\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{y}}\right)\mathrm{dy}\:=\int\left(\frac{\mathrm{1}}{\mathrm{y}}−\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}\right)\mathrm{dy} \\ $$$$=\mathrm{ln}\mid\frac{\mathrm{y}}{\mathrm{y}−\mathrm{1}}\mid\:\Rightarrow\mathrm{ln}\mid\frac{\mathrm{y}}{\mathrm{y}−\mathrm{1}}\mid\:=\mathrm{ln}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{c}\:\Rightarrow\mid\frac{\mathrm{y}}{\mathrm{y}−\mathrm{1}}\mid\:=\mathrm{k}\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{y}}{\mathrm{y}−\mathrm{1}}\:=\mathrm{k}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{y}−\mathrm{1}+\mathrm{1}}{\mathrm{y}−\mathrm{1}}\:=\mathrm{k}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{1}+\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}\:=\mathrm{k}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}\:=\mathrm{k}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\:\Rightarrow\mathrm{y}−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{k}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{1}}\:\Rightarrow\mathrm{y}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *