Question Number 92923 by Ar Brandon last updated on 09/May/20
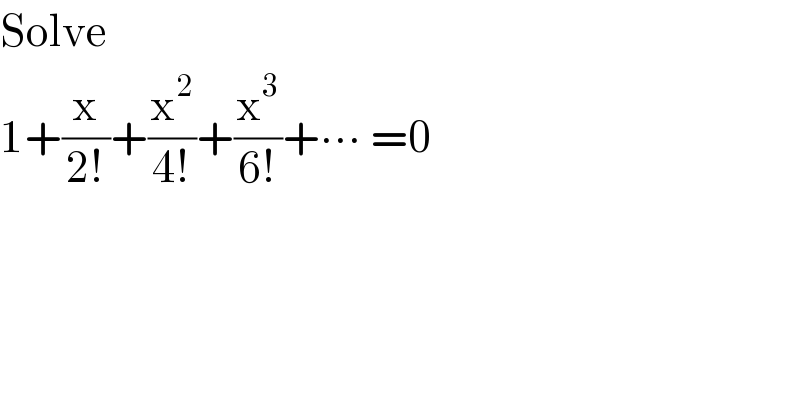
$$\mathrm{Solve} \\ $$$$\mathrm{1}+\frac{\mathrm{x}}{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}!}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}!}+\centerdot\centerdot\centerdot\:=\mathrm{0} \\ $$
Answered by mr W last updated on 09/May/20
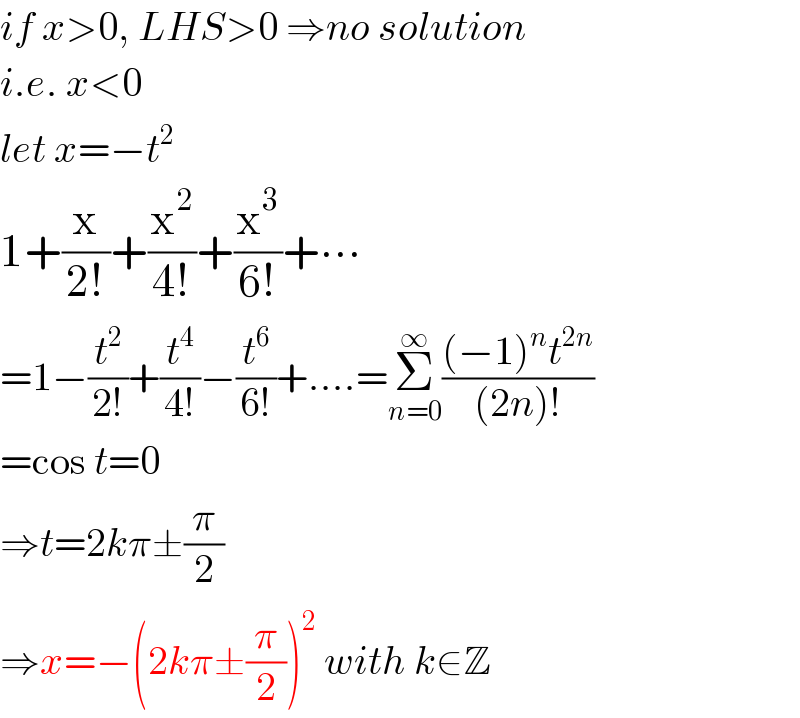
$${if}\:{x}>\mathrm{0},\:{LHS}>\mathrm{0}\:\Rightarrow{no}\:{solution} \\ $$$${i}.{e}.\:{x}<\mathrm{0} \\ $$$${let}\:{x}=−{t}^{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{x}}{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}!}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}!}+\centerdot\centerdot\centerdot\: \\ $$$$=\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{t}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{t}^{\mathrm{6}} }{\mathrm{6}!}+….=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {t}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$=\mathrm{cos}\:{t}=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{2}{k}\pi\pm\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{x}=−\left(\mathrm{2}{k}\pi\pm\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} \:{with}\:{k}\in\mathbb{Z} \\ $$
Commented by Ar Brandon last updated on 09/May/20
��yes !
