Menu Close

solve-1-x-2-y-1-x-2-y-x-e-3x-

Tinku Tara 0 Comments
Pin




Question Number 61178 by mathsolverby Abdo last updated on 30/May/19
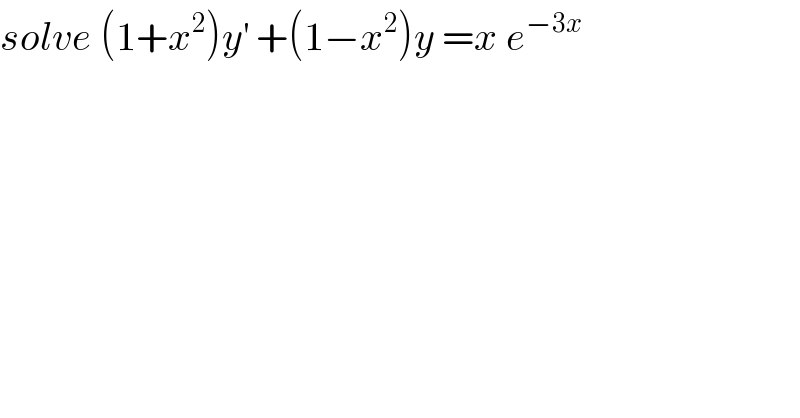
solve (1+x^2 )y^′ +(1−x^2 )y =x e^(−3x)
$${solve}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}\:={x}\:{e}^{−\mathrm{3}{x}} \\ $$
Commented by maxmathsup by imad last updated on 31/May/19
(he)→(1+x^2 )y^′ +(1−x^2 )y =0 ⇒(1+x^2 )y^′ =(x^2 −1)y ⇒ (y^′ /y) =((x^2 −1)/(x^2 +1)) ⇒ln∣y∣ =∫ ((x^2 −1)/(x^2 +1)) dx +c =∫ ((x^2 +1−2)/(x^2 +1)) dx +c =x−2arctan(x)+c ⇒ y(x) =K e^(x−2arctan(x)) mvc method give y^′ =K^′ e^(x−2arctan(x)) +K (1−(2/(1+x^2 )))e^(x−2arctan(x)) =(K^′ +K((x^2 −1)/(x^2 +2)))e^(x−2arctan(x)) (e)⇒(1+x^2 )K^′ e^(x−2arctan(x)) +K(x^2 −1) e^(x−2arctan(x)) +(1−x^2 )K e^(x−2arctan(x)) =x e^(−3x) ⇒ (1+x^2 )K^′ e^(x−2arctan(x)) =x e^(−3x) ⇒K^′ =(x/(1+x^2 )) e^(−3x−x +2arctan(x)) =(x/(1+x^2 )) e^(−4x +2arctan(x)) ⇒K(x) =∫ ((x e^(−4x +2arctan(x)) )/(1+x^2 )) dx +λ⇒ y(x) =( ∫ ((x e^(−4x +2arctan(x)) )/(1+x^2 ))dx +λ)e^(x−2arctan(x)) =λ e^(x−2arctan(x)) +e^(x−2arctan(x)) ∫_. ^x ((t e^(−4t +2arctan(t)) )/(1+t^2 )) dt ( λ ∈R).
$$\left({he}\right)\rightarrow\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:=\left({x}^{\mathrm{2}} −\mathrm{1}\right){y}\:\Rightarrow \\ $$$$\frac{{y}^{'} }{{y}}\:=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{ln}\mid{y}\mid\:=\int\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:+{c} \\ $$$$=\int\:\frac{{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:+{c}\:={x}−\mathrm{2}{arctan}\left({x}\right)+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)\:={K}\:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:\:\:\:{mvc}\:{method}\:{give} \\ $$$${y}^{'} \:={K}^{'} \:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:+{K}\:\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \\ $$$$=\left({K}^{'} \:+{K}\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{2}}\right){e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \\ $$$$\left({e}\right)\Rightarrow\left(\mathrm{1}+{x}^{\mathrm{2}} \right){K}^{'} \:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:+{K}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \\ $$$$+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){K}\:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:={x}\:{e}^{−\mathrm{3}{x}} \:\Rightarrow \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){K}^{'} \:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:={x}\:{e}^{−\mathrm{3}{x}} \:\Rightarrow{K}^{'} \:=\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{e}^{−\mathrm{3}{x}−{x}\:+\mathrm{2}{arctan}\left({x}\right)} \\ $$$$=\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{e}^{−\mathrm{4}{x}\:+\mathrm{2}{arctan}\left({x}\right)} \Rightarrow{K}\left({x}\right)\:=\int\:\:\frac{{x}\:{e}^{−\mathrm{4}{x}\:+\mathrm{2}{arctan}\left({x}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:+\lambda\Rightarrow \\ $$$${y}\left({x}\right)\:=\left(\:\int\:\:\frac{{x}\:{e}^{−\mathrm{4}{x}\:+\mathrm{2}{arctan}\left({x}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:+\lambda\right){e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \\ $$$$=\lambda\:{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:\:+{e}^{{x}−\mathrm{2}{arctan}\left({x}\right)} \:\int_{.} ^{{x}} \:\:\:\frac{{t}\:{e}^{−\mathrm{4}{t}\:+\mathrm{2}{arctan}\left({t}\right)} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:\:\left(\:\lambda\:\in{R}\right). \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *