Menu Close

Solve-1-x-2-y-4xy-6y-0-

Tinku Tara 0 Comments
Pin




Question Number 100337 by I want to learn more last updated on 26/Jun/20
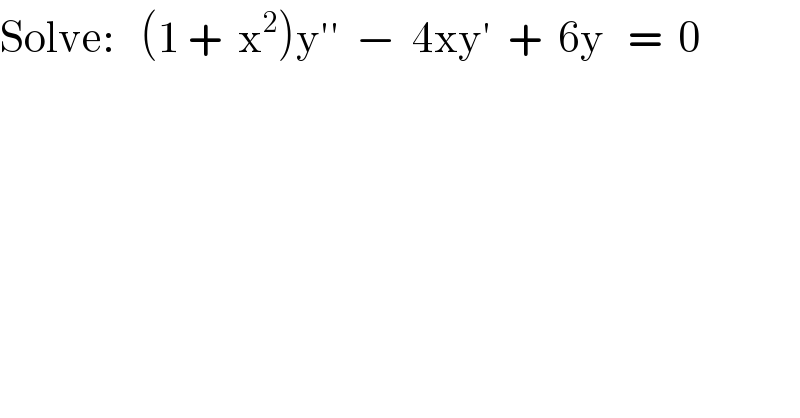
Solve: (1 + x^2 )y′′ − 4xy′ + 6y = 0
$$\mathrm{Solve}:\:\:\:\left(\mathrm{1}\:+\:\:\mathrm{x}^{\mathrm{2}} \right)\mathrm{y}''\:\:−\:\:\mathrm{4xy}'\:\:+\:\:\mathrm{6y}\:\:\:=\:\:\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 26/Jun/20
let determine a solution develppsble at integr serie y =Σ_(n=0) ^(∞ ) a_n x^n ⇒y^′ =Σ_(n=1) ^∞ na_n x^(n−1) ⇒y^(′′) =Σ_(n=2) ^∞ n(n−1)a_n x^(n−2) e⇒(1+x^2 )Σ_(n=2) ^∞ n(n−1)a_n x^(n−2) −4x Σ_(n=1) ^∞ na_n x^(n−1) +6Σ_(n=0) ^∞ a_n x^(n ) =0 ⇒ Σ_(n=2) ^∞ n(n−1)a_n x^(n−2) +Σ_(n=2) ^∞ n(n−1)a_n x^n −4Σ_(n=1) ^∞ na_n x^n +6 Σ_(n=0) ^∞ a_n x^n =0 ⇒ Σ_(n=0) ^∞ (n+2)(n+1)a_(n+2) x^n +Σ_(n=1) ^∞ (n^2 a_n −na_n −4na_n +6a_n )x^n +6a_0 =0 ⇒ +Σ_(n=1) ^∞ {(n+1)(n+2)a_(n+2) +(n^2 −5n +6)a_n }x^n +6a_0 +2a_2 =0 ⇒ ⇒ { (((n+1)(n+2)a_(n+2) +(n^2 −5n+6)a_n =0)),((3a_0 +a_2 =0)) :} ⇒ { ((a_(n+2) =−((n^2 −5n+6)/(n^2 +3n +2))a_n )),((a_2 =−3a_0 )) :} and from this relation we calculate a_(2n) and a_(2n+1) ....
$$\mathrm{let}\:\mathrm{determine}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{develppsble}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie}\:\mathrm{y}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{y}^{'} \:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{na}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\mathrm{y}^{''} \:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{e}\Rightarrow\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}−\mathrm{2}} \:−\mathrm{4x}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{na}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \:+\mathrm{6}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}\:} \:=\mathrm{0}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}−\mathrm{2}} \:+\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \:−\mathrm{4}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{na}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \:+\mathrm{6}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \:=\mathrm{0}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}_{\mathrm{n}+\mathrm{2}} \mathrm{x}^{\mathrm{n}} \:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{n}^{\mathrm{2}} \mathrm{a}_{\mathrm{n}} −\mathrm{na}_{\mathrm{n}} −\mathrm{4na}_{\mathrm{n}} \:+\mathrm{6a}_{\mathrm{n}} \right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{6a}_{\mathrm{0}} =\mathrm{0}\:\Rightarrow \\ $$$$\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left\{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\mathrm{a}_{\mathrm{n}+\mathrm{2}} +\left(\mathrm{n}^{\mathrm{2}} −\mathrm{5n}\:+\mathrm{6}\right)\mathrm{a}_{\mathrm{n}} \right\}\mathrm{x}^{\mathrm{n}} \:+\mathrm{6a}_{\mathrm{0}} \:+\mathrm{2a}_{\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\begin{cases}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\mathrm{a}_{\mathrm{n}+\mathrm{2}} \:+\left(\mathrm{n}^{\mathrm{2}} −\mathrm{5n}+\mathrm{6}\right)\mathrm{a}_{\mathrm{n}} =\mathrm{0}}\\{\mathrm{3a}_{\mathrm{0}} \:+\mathrm{a}_{\mathrm{2}} =\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}_{\mathrm{n}+\mathrm{2}} =−\frac{\mathrm{n}^{\mathrm{2}} −\mathrm{5n}+\mathrm{6}}{\mathrm{n}^{\mathrm{2}} \:+\mathrm{3n}\:+\mathrm{2}}\mathrm{a}_{\mathrm{n}} }\\{\mathrm{a}_{\mathrm{2}} =−\mathrm{3a}_{\mathrm{0}} }\end{cases} \\ $$$$\mathrm{and}\:\mathrm{from}\:\mathrm{this}\:\mathrm{relation}\:\mathrm{we}\:\mathrm{calculate}\:\mathrm{a}_{\mathrm{2n}} \:\mathrm{and}\:\mathrm{a}_{\mathrm{2n}+\mathrm{1}} …. \\ $$
Commented by I want to learn more last updated on 26/Jun/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by maths mind last updated on 26/Jun/20
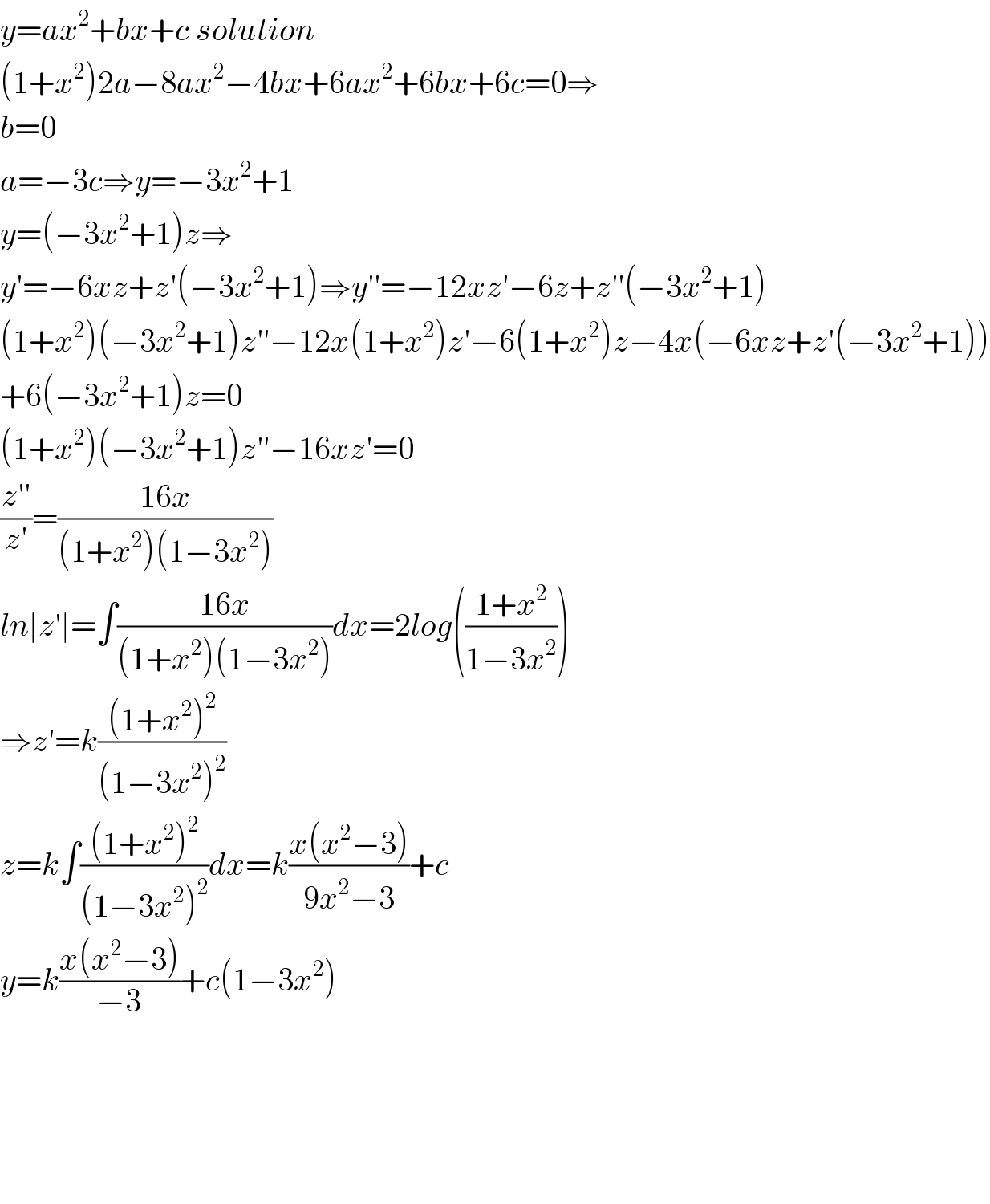
y=ax^2 +bx+c solution (1+x^2 )2a−8ax^2 −4bx+6ax^2 +6bx+6c=0⇒ b=0 a=−3c⇒y=−3x^2 +1 y=(−3x^2 +1)z⇒ y′=−6xz+z′(−3x^2 +1)⇒y′′=−12xz′−6z+z′′(−3x^2 +1) (1+x^2 )(−3x^2 +1)z′′−12x(1+x^2 )z′−6(1+x^2 )z−4x(−6xz+z′(−3x^2 +1)) +6(−3x^2 +1)z=0 (1+x^2 )(−3x^2 +1)z′′−16xz′=0 ((z′′)/(z′))=((16x)/((1+x^2 )(1−3x^2 ))) ln∣z′∣=∫((16x)/((1+x^2 )(1−3x^2 )))dx=2log(((1+x^2 )/(1−3x^2 ))) ⇒z′=k(((1+x^2 )^2 )/((1−3x^2 )^2 )) z=k∫(((1+x^2 )^2 )/((1−3x^2 )^2 ))dx=k((x(x^2 −3))/(9x^2 −3))+c y=k((x(x^2 −3))/(−3))+c(1−3x^2 )
$${y}={ax}^{\mathrm{2}} +{bx}+{c}\:{solution} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mathrm{2}{a}−\mathrm{8}{ax}^{\mathrm{2}} −\mathrm{4}{bx}+\mathrm{6}{ax}^{\mathrm{2}} +\mathrm{6}{bx}+\mathrm{6}{c}=\mathrm{0}\Rightarrow \\ $$$${b}=\mathrm{0} \\ $$$${a}=−\mathrm{3}{c}\Rightarrow{y}=−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${y}=\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right){z}\Rightarrow \\ $$$${y}'=−\mathrm{6}{xz}+{z}'\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\Rightarrow{y}''=−\mathrm{12}{xz}'−\mathrm{6}{z}+{z}''\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right){z}''−\mathrm{12}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){z}'−\mathrm{6}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){z}−\mathrm{4}{x}\left(−\mathrm{6}{xz}+{z}'\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)\right) \\ $$$$+\mathrm{6}\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right){z}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right){z}''−\mathrm{16}{xz}'=\mathrm{0} \\ $$$$\frac{{z}''}{{z}'}=\frac{\mathrm{16}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right)} \\ $$$${ln}\mid{z}'\mid=\int\frac{\mathrm{16}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right)}{dx}=\mathrm{2}{log}\left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{z}'={k}\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${z}={k}\int\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}={k}\frac{{x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)}{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{3}}+{c} \\ $$$${y}={k}\frac{{x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)}{−\mathrm{3}}+{c}\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by I want to learn more last updated on 28/Jun/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *