Question Number 15095 by tawa tawa last updated on 07/Jun/17
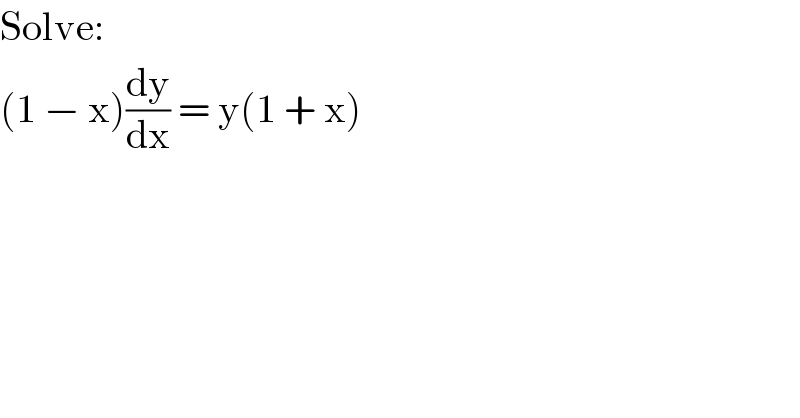
$$\mathrm{Solve}: \\ $$$$\left(\mathrm{1}\:−\:\mathrm{x}\right)\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{y}\left(\mathrm{1}\:+\:\mathrm{x}\right) \\ $$
Answered by Tinkutara last updated on 07/Jun/17
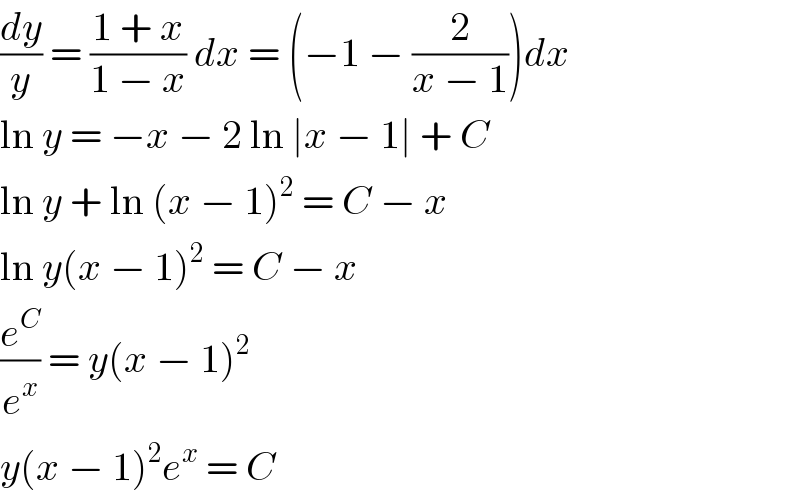
$$\frac{{dy}}{{y}}\:=\:\frac{\mathrm{1}\:+\:{x}}{\mathrm{1}\:−\:{x}}\:{dx}\:=\:\left(−\mathrm{1}\:−\:\frac{\mathrm{2}}{{x}\:−\:\mathrm{1}}\right){dx} \\ $$$$\mathrm{ln}\:{y}\:=\:−{x}\:−\:\mathrm{2}\:\mathrm{ln}\:\mid{x}\:−\:\mathrm{1}\mid\:+\:{C} \\ $$$$\mathrm{ln}\:{y}\:+\:\mathrm{ln}\:\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:{C}\:−\:{x} \\ $$$$\mathrm{ln}\:{y}\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:{C}\:−\:{x} \\ $$$$\frac{{e}^{{C}} }{{e}^{{x}} }\:=\:{y}\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} \\ $$$${y}\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} {e}^{{x}} \:=\:{C} \\ $$
Commented by tawa tawa last updated on 07/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
