Menu Close

solve-1-y-3-y-2-y-2-0-2-4y-x-2-y-2-

Tinku Tara 0 Comments
Pin




Question Number 126758 by bounhome last updated on 24/Dec/20
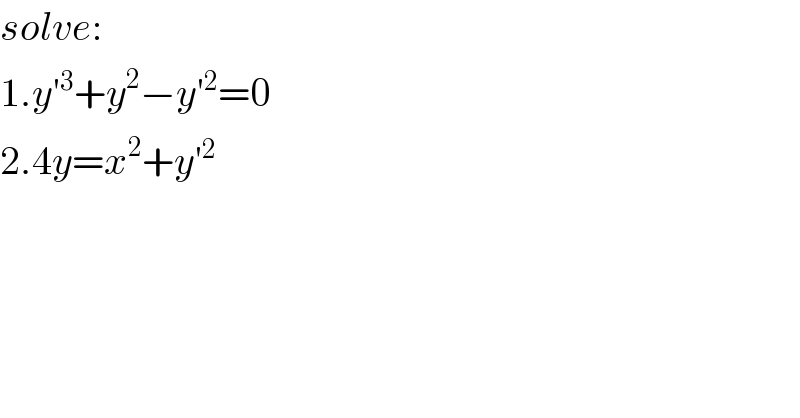
solve: 1.y′^3 +y^2 −y′^2 =0 2.4y=x^2 +y′^2
$${solve}: \\ $$$$\mathrm{1}.{y}'^{\mathrm{3}} +{y}^{\mathrm{2}} −{y}'^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}.\mathrm{4}{y}={x}^{\mathrm{2}} +{y}'^{\mathrm{2}} \\ $$
Answered by liberty last updated on 24/Dec/20
(2) ((dy/dx))^2 = 4y−x^2 (dy/dx) = ± (√(4y−x^2 )) let y = u^2 x^2 →(dy/dx) = 2xu^2 +2x^2 u (du/dx) ⇔ 2xu^2 +2x^2 u (du/dx) = ± x(√(4u^2 −1)) ⇔ 2xu (du/dx) = ±(√(4u^2 −1))−2u^2 ((2u)/(±(√(4u^2 −1))−2u^2 )) du= (dx/x) (1) ∫ ((2u)/( (√(4u^2 −1))−2u^2 )) du = ln Cx let tan w = (√(4u^2 −1)) ∫ ((−2w dw)/(w^2 −2w+1)) = ln Cx −∫ ((d(w^2 −2w+1))/(w^2 −2w+1)) −∫ (2/((w−1)^2 ))dw = ln Cx −2ln ∣w−1∣+(2/(w−1)) = ln Cx (2/(tan^(−1) ((√(4u^2 −1)))−1)) = ln (Cx(tan^(−1) ((√(4u^2 −1))−1)^2 ) (2/(tan^(−1) ((√((4y−x^2 )/x^2 )))−1)) = ln (Cx (tan^(−1) ((√((4y−x^2 )/x^2 )))−1)^2 )
$$\left(\mathrm{2}\right)\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\:\mathrm{4}{y}−{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\frac{{dy}}{{dx}}\:=\:\pm\:\sqrt{\mathrm{4}{y}−{x}^{\mathrm{2}} } \\ $$$$\:{let}\:{y}\:=\:{u}^{\mathrm{2}} {x}^{\mathrm{2}} \:\rightarrow\frac{{dy}}{{dx}}\:=\:\mathrm{2}{xu}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} {u}\:\frac{{du}}{{dx}} \\ $$$$\Leftrightarrow\:\mathrm{2}{xu}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} {u}\:\frac{{du}}{{dx}}\:=\:\pm\:{x}\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Leftrightarrow\:\mathrm{2}{xu}\:\frac{{du}}{{dx}}\:=\:\pm\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2}{u}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}{u}}{\pm\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2}{u}^{\mathrm{2}} }\:{du}=\:\frac{{dx}}{{x}} \\ $$$$\left(\mathrm{1}\right)\:\int\:\frac{\mathrm{2}{u}}{\:\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2}{u}^{\mathrm{2}} }\:{du}\:=\:\mathrm{ln}\:{Cx}\: \\ $$$$\:\:\:\:{let}\:\mathrm{tan}\:{w}\:=\:\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\int\:\frac{−\mathrm{2}{w}\:{dw}}{{w}^{\mathrm{2}} −\mathrm{2}{w}+\mathrm{1}}\:=\:\mathrm{ln}\:{Cx} \\ $$$$\:−\int\:\frac{{d}\left({w}^{\mathrm{2}} −\mathrm{2}{w}+\mathrm{1}\right)}{{w}^{\mathrm{2}} −\mathrm{2}{w}+\mathrm{1}}\:−\int\:\frac{\mathrm{2}}{\left({w}−\mathrm{1}\right)^{\mathrm{2}} }{dw}\:=\:\mathrm{ln}\:{Cx} \\ $$$$−\mathrm{2ln}\:\mid{w}−\mathrm{1}\mid+\frac{\mathrm{2}}{{w}−\mathrm{1}}\:=\:\mathrm{ln}\:{Cx} \\ $$$$\:\:\:\frac{\mathrm{2}}{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}}\right)−\mathrm{1}}\:=\:\mathrm{ln}\:\left({Cx}\left(\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} \right)\right. \\ $$$$\:\frac{\mathrm{2}}{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{4}{y}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\right)−\mathrm{1}}\:=\:\mathrm{ln}\:\left({Cx}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{4}{y}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\right)−\mathrm{1}\right)^{\mathrm{2}} \right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *