Question Number 14757 by RasheedSoomro last updated on 04/Jun/17
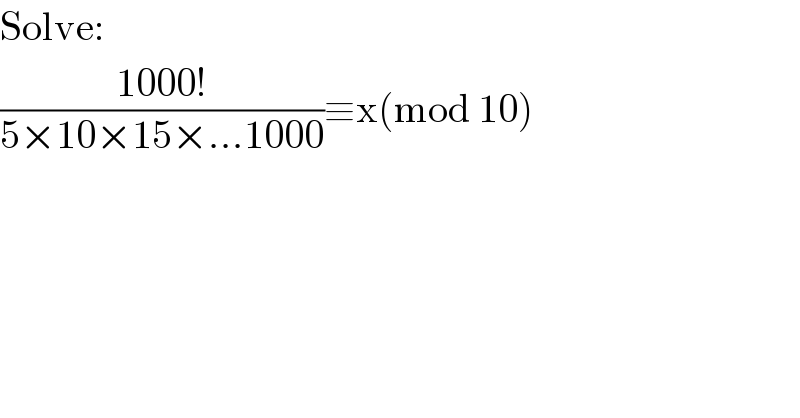
$$\mathrm{Solve}: \\ $$$$\frac{\mathrm{1000}!}{\mathrm{5}×\mathrm{10}×\mathrm{15}×…\mathrm{1000}}\equiv\mathrm{x}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$
Answered by RasheedSoomro last updated on 05/Jun/17

$$\mathrm{x}\equiv\frac{\mathrm{1000}!}{\mathrm{5}×\mathrm{10}×\mathrm{15}×…\mathrm{1000}}\left(\mathrm{mod}\:\mathrm{10}\right. \\ $$$$\mathrm{x}\equiv\left(\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}\right)\left(\mathrm{6}.\mathrm{7}.\mathrm{8}.\mathrm{9}\right)…\left(\mathrm{996}.\mathrm{997}.\mathrm{998}.\mathrm{999}\right)\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\mathrm{In}\:\mathrm{brackets}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{of}\:\mathrm{5k}+\mathrm{1},\mathrm{5k}+\mathrm{2},\mathrm{5k}+\mathrm{3}\:\mathrm{and} \\ $$$$\mathrm{5k}+\mathrm{4}\:\mathrm{types}.\:\mathrm{The}\:\mathrm{following}\:\mathrm{can}\:\mathrm{be}\:\mathrm{proved} \\ $$$$\left(\mathrm{5k}+\mathrm{1}\right)\left(\mathrm{5k}+\mathrm{2}\right)\left(\mathrm{5k}+\mathrm{3}\right)\left(\mathrm{5k}+\mathrm{4}\right)\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{See}\:\mathrm{answer}\:\mathrm{of}\:\mathrm{mrW1}\:\mathrm{to}\:\mathrm{Q}#\mathrm{14614}\right) \\ $$$$\mathrm{Hence}\: \\ $$$$\:\:\:\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\:\:\:\mathrm{6}.\mathrm{7}.\mathrm{8}.\mathrm{9}\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\:\:\:\:\vdots \\ $$$$\:\:\mathrm{996}.\mathrm{997}.\mathrm{998}.\mathrm{999}\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{Total}\:\mathrm{congruences}=\mathrm{200}\:\left(\mathrm{2}\:\mathrm{per}\:\mathrm{each}\:\mathrm{ten}\right) \\ $$$$\mathrm{Multiplying}\:\mathrm{all}\:\mathrm{the}\:\mathrm{200}\:\mathrm{congruences} \\ $$$$\left(\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}\right)\left(\mathrm{6}.\mathrm{7}.\mathrm{8}.\mathrm{9}\right)…\left(\mathrm{996}.\mathrm{997}.\mathrm{998}.\mathrm{999}\right)\equiv\mathrm{4}^{\mathrm{200}} \equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\left(\mathrm{4}^{\mathrm{1}} \equiv\mathrm{4},\mathrm{4}^{\mathrm{2}} \equiv\mathrm{6},\mathrm{4}^{\mathrm{3}} \equiv\mathrm{4},\:…,\mathrm{4}^{\mathrm{2k}+\mathrm{1}} \equiv\mathrm{4},\mathrm{4}^{\mathrm{2k}} \equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{10}\right)\:\:\right) \\ $$$$\mathrm{So}\:\frac{\mathrm{1000}!}{\mathrm{5}×\mathrm{10}×\mathrm{15}×…\mathrm{1000}}\equiv\mathrm{6}\:\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$ \\ $$
Commented by RasheedSoomro last updated on 05/Jun/17

$$\mathrm{Now},\:\mathrm{I}\:\mathrm{think},\:\mathrm{I}'\mathrm{m}\:\mathrm{able}\:\mathrm{to}\:\mathrm{answer} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{of}\:\boldsymbol{\mathrm{prakash}}\:\boldsymbol{\mathrm{jain}}. \\ $$$$\left(\mathrm{To}\:\mathrm{determine}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}…\right) \\ $$$$\mathrm{Q}#\mathrm{13724} \\ $$
Commented by RasheedSoomro last updated on 05/Jun/17

$$\mathrm{To}\:\boldsymbol{\mathrm{S}}\mathrm{ir}\:\mathrm{prakash}\:\mathrm{jain}\:\&\:\mathrm{mrW1} \\ $$$$\&\:\mathrm{All}\:\mathrm{who}\:\mathrm{are}\:\mathrm{interested}\:\mathrm{in}\:\boldsymbol{\mathrm{Number}}\:\boldsymbol{\mathrm{Theory}}. \\ $$$$\mathrm{Pl}\:\mathrm{see}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{your}\:\mathrm{Q}#\mathrm{13724} \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{solve}.\:\mathrm{The}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{based}\:\mathrm{on}\:\mathrm{the}\:\mathrm{above}\:\mathrm{answer}. \\ $$
Commented by mrW1 last updated on 05/Jun/17

$${nice}\:{work}! \\ $$$$ \\ $$$$\frac{\mathrm{1000}!}{\mathrm{5}×\mathrm{10}×\mathrm{15}×…\mathrm{1000}}\equiv\mathrm{6}\:\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$ \\ $$$${I}\:{can}\:{confirm}\:{this}\:{through}\:{a}\:{different} \\ $$$${way}: \\ $$$$ \\ $$$${in}\:\mathrm{1000}!\:{there}\:{are}\:\mathrm{100}\:{numbers}\:{which} \\ $$$${end}\:{with}\:\mathrm{1}:\:\mathrm{1},\mathrm{11},\mathrm{21},…\mathrm{101},\mathrm{111},…\mathrm{991} \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{1} \\ $$$$ \\ $$$${similarly}\:{there}\:{are}\:\mathrm{100}\:{numbers}\:{ending} \\ $$$${with}\:\mathrm{2}:\:\mathrm{2},\mathrm{12},\mathrm{22},…,\mathrm{102},\mathrm{112},…,\mathrm{992} \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{6} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{100}\:{numbers}\:{ending}\:{with}\:\mathrm{3}, \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{1} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{100}\:{numbers}\:{ending}\:{with}\:\mathrm{4}, \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{6} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{100}\:{numbers}\:{ending}\:{with}\:\mathrm{6}, \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{6} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{100}\:{numbers}\:{ending}\:{with}\:\mathrm{7}, \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{1} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{100}\:{numbers}\:{ending}\:{with}\:\mathrm{8}, \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{6} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{100}\:{numbers}\:{ending}\:{with}\:\mathrm{9}, \\ $$$${the}\:{product}\:{of}\:{them}\:{ends}\:{with}\:\mathrm{1} \\ $$$$ \\ $$$${these}\:{values}\:{end}\:{with}\:\mathrm{1}\:{or}\:\mathrm{6},\:{so}\:{their} \\ $$$${product}\:{will}\:{also}\:{end}\:{with}\:\mathrm{6}. \\ $$$$ \\ $$$${that}\:{means}\:{if}\:{we}\:{exclude}\:{the}\:{numbers} \\ $$$$\mathrm{10},\mathrm{20},…,\mathrm{100},\mathrm{110},…,\mathrm{990},\mathrm{1000}\:{and} \\ $$$$\mathrm{5},\mathrm{15},\mathrm{25},…,\mathrm{105},\mathrm{115},…,\mathrm{995},\:{the}\:{product} \\ $$$${of}\:{the}\:{remaining}\:{numbers}\:{in}\:\mathrm{1000}!\: \\ $$$${will}\:{end}\:{with}\:{the}\:{digit}\:\mathrm{6}. \\ $$
Commented by RasheedSoomro last updated on 05/Jun/17

$$\boldsymbol{\mathcal{TH}\alpha{nksA}\mathcal{LOT}}\:\:\boldsymbol{\mathcal{S}{ir}}\:! \\ $$$$\boldsymbol{\mathcal{N}{ice\&easy}}\:\:\boldsymbol{{method}}! \\ $$
