Question Number 104475 by pete last updated on 21/Jul/20
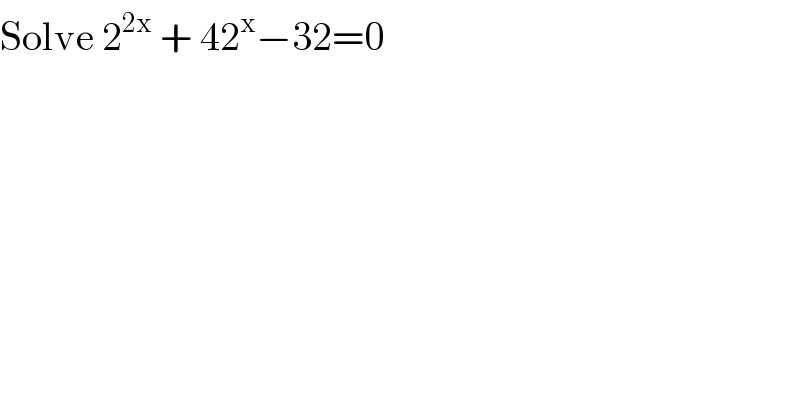
$$\mathrm{Solve}\:\mathrm{2}^{\mathrm{2x}} \:+\:\mathrm{42}^{\mathrm{x}} −\mathrm{32}=\mathrm{0} \\ $$
Answered by $@y@m last updated on 21/Jul/20

$${I}\:{think}\:{there}\:{is}\:{a}\:{typo}\:{in}\:{question}. \\ $$$${It}\:{should}\:{be}: \\ $$$$\mathrm{Solve}\:\mathrm{2}^{\mathrm{2x}} \:+\:\mathrm{4}.\mathrm{2}^{\mathrm{x}} −\mathrm{32}=\mathrm{0} \\ $$$${Solution}:\:{Let}\:\mathrm{2}^{{x}} ={y} \\ $$$${y}^{\mathrm{2}} +\mathrm{4}{y}−\mathrm{32}=\mathrm{0} \\ $$$${y}=\mathrm{4},−\mathrm{8} \\ $$$${But}\:{y}=−\mathrm{8}\:{is}\:{inadmissible}. \\ $$$$\therefore\:{y}=\mathrm{4} \\ $$$${x}=\mathrm{2} \\ $$
Commented by pete last updated on 21/Jul/20
$$\mathrm{ok}\:\mathrm{thanks}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jul/20
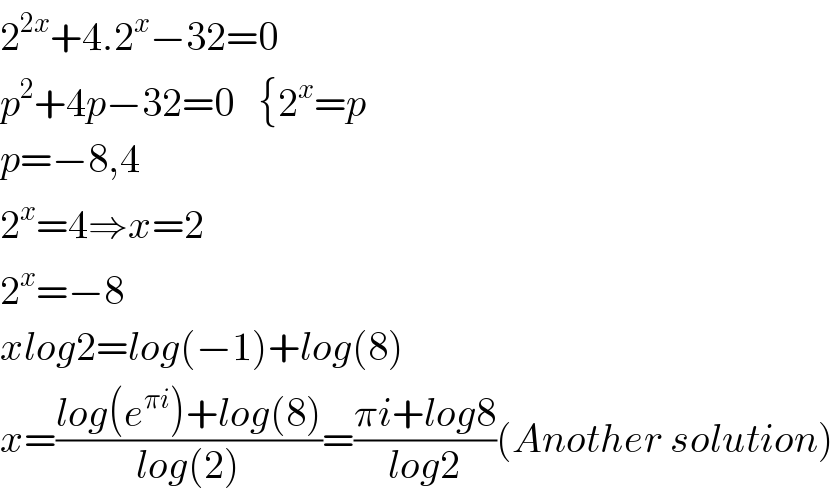
$$\mathrm{2}^{\mathrm{2}{x}} +\mathrm{4}.\mathrm{2}^{{x}} −\mathrm{32}=\mathrm{0} \\ $$$${p}^{\mathrm{2}} +\mathrm{4}{p}−\mathrm{32}=\mathrm{0}\:\:\:\left\{\mathrm{2}^{{x}} ={p}\right. \\ $$$${p}=−\mathrm{8},\mathrm{4} \\ $$$$\mathrm{2}^{{x}} =\mathrm{4}\Rightarrow{x}=\mathrm{2} \\ $$$$\mathrm{2}^{{x}} =−\mathrm{8} \\ $$$${xlog}\mathrm{2}={log}\left(−\mathrm{1}\right)+{log}\left(\mathrm{8}\right) \\ $$$${x}=\frac{{log}\left({e}^{\pi{i}} \right)+{log}\left(\mathrm{8}\right)}{{log}\left(\mathrm{2}\right)}=\frac{\pi{i}+{log}\mathrm{8}}{{log}\mathrm{2}}\left({Another}\:{solution}\right) \\ $$
Commented by $@y@m last updated on 22/Jul/20

