Question Number 96650 by bobhans last updated on 03/Jun/20
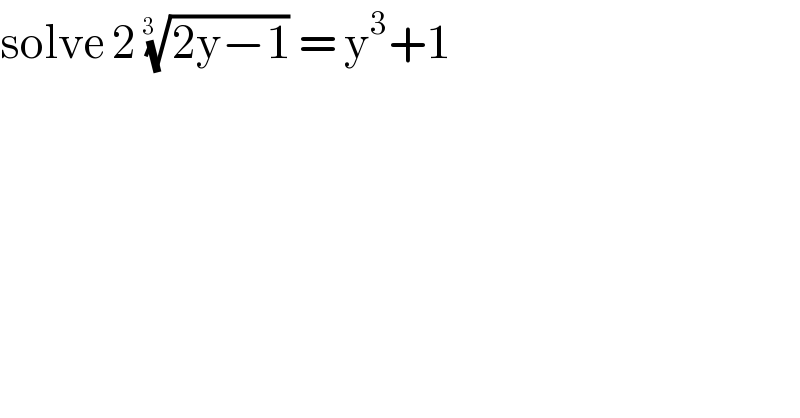
$$\mathrm{solve}\:\mathrm{2}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2y}−\mathrm{1}}\:=\:\mathrm{y}^{\mathrm{3}} +\mathrm{1} \\ $$
Answered by john santu last updated on 03/Jun/20

$$\sqrt[{\mathrm{3}\:\:}]{\mathrm{2y}−\mathrm{1}}\:=\:\frac{\mathrm{y}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}^{−\mathrm{1}} \left(\mathrm{y}\right)=\mathrm{f}\left(\mathrm{y}\right)\:\Rightarrow\mathrm{y}=\frac{\mathrm{y}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{3}} −\mathrm{2y}+\mathrm{1}=\mathrm{0}\:;\:\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{y}=\mathrm{1}}\\{\mathrm{y}=\frac{−\mathrm{1}\:\pm\:\sqrt{\mathrm{5}}}{\mathrm{2}}\:}\end{cases} \\ $$
