Question Number 98967 by M±th+et+s last updated on 17/Jun/20
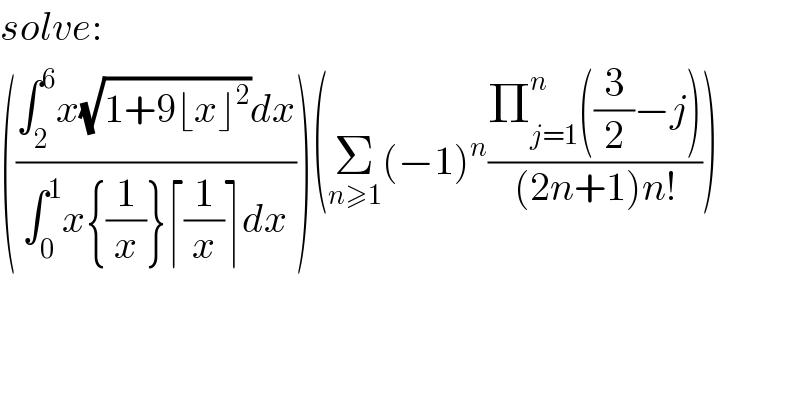
$${solve}: \\ $$$$\left(\frac{\int_{\mathrm{2}} ^{\mathrm{6}} {x}\sqrt{\mathrm{1}+\mathrm{9}\lfloor{x}\rfloor^{\mathrm{2}} }{dx}}{\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left\{\frac{\mathrm{1}}{{x}}\right\}\lceil\frac{\mathrm{1}}{{x}}\rceil{dx}}\right)\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{\prod_{{j}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{3}}{\mathrm{2}}−{j}\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\right) \\ $$
Answered by maths mind last updated on 17/Jun/20
![Σ_(n≥1) (−1)^n .((Π_(j=1) ^n ((3/2)−j))/((2n+1)n!))=Σ_(n≥1) (((−1)^n .Π_(j=0) ^(n−1) (j−(1/2)).Π_(j=0) ^(n−1) (j+(1/2)))/(Π_(j=0) ^(n−1) ((3/2)+j).n!)) =_2 F_1 (−(1/2),(1/2);(3/2);−1)=(1/(β((1/2),1))) ∫_0 ^1 x^(−(1/2)) .(1−x)^((3/2)−(1/2)−1) (1+x)^(1/2) dx =((Γ((3/2)))/(Γ((1/2))Γ(1))).∫_0 ^1 (√((x+1)/x))dx easy now ∫_0 ^1 x{(1/x)}[(1/x)] dx=∫_1 ^(+∞) (({y}[y])/y^3 )dy =Σ_(n≥1) ∫_n ^(n+1) (((y−[y]][y])/y^3 )dy =Σ_(n≥1) ∫_n ^(n+1) ((n/y^2 )−(n^2 /y^3 ))dy =Σ_(n≥1) [−(n/(n+1))+1+(1/2)(n^2 /((n+1)^2 ))−(n^2 /(2n^2 ))] =Σ_(n≥1) (((−2n(n+1)+(n+1)^2 +n^2 )/(2(n+1)^2 ))=(1/2)Σ_(n≥1) (1/((n+1)^2 ))=((ζ(2)−1)/2)=(π^2 /(12))−(1/2) just ∫_2 ^6 x(√(1+9[x]^2 ))dx easy one](https://www.tinkutara.com/question/Q98977.png)
$$\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}} .\frac{\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{\mathrm{3}}{\mathrm{2}}−{j}\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} .\underset{{j}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({j}−\frac{\mathrm{1}}{\mathrm{2}}\right).\underset{{j}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({j}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\underset{{j}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\frac{\mathrm{3}}{\mathrm{2}}+{j}\right).{n}!} \\ $$$$=_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};−\mathrm{1}\right)=\frac{\mathrm{1}}{\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right)}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{1}}{\mathrm{2}}} .\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}\right)}.\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{{x}+\mathrm{1}}{{x}}}{dx} \\ $$$${easy}\:{now} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left\{\frac{\mathrm{1}}{{x}}\right\}\left[\frac{\mathrm{1}}{{x}}\right]\:{dx}=\int_{\mathrm{1}} ^{+\infty} \frac{\left\{{y}\right\}\left[{y}\right]}{{y}^{\mathrm{3}} }{dy} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{{n}} ^{{n}+\mathrm{1}} \frac{\left({y}−\left[{y}\right]\right]\left[{y}\right]}{{y}^{\mathrm{3}} }{dy} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{{n}} ^{{n}+\mathrm{1}} \left(\frac{{n}}{{y}^{\mathrm{2}} }−\frac{{n}^{\mathrm{2}} }{{y}^{\mathrm{3}} }\right){dy} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\left[−\frac{{n}}{{n}+\mathrm{1}}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\frac{{n}^{\mathrm{2}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{{n}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{2}} }\right] \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{2}{n}\left({n}+\mathrm{1}\right)+\left({n}+\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} \right.}{\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\zeta\left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{2}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${just}\:\int_{\mathrm{2}} ^{\mathrm{6}} {x}\sqrt{\mathrm{1}+\mathrm{9}\left[{x}\right]^{\mathrm{2}} }{dx}\:{easy}\:{one} \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 17/Jun/20
well done ����������
