Question Number 129613 by mohammad17 last updated on 16/Jan/21
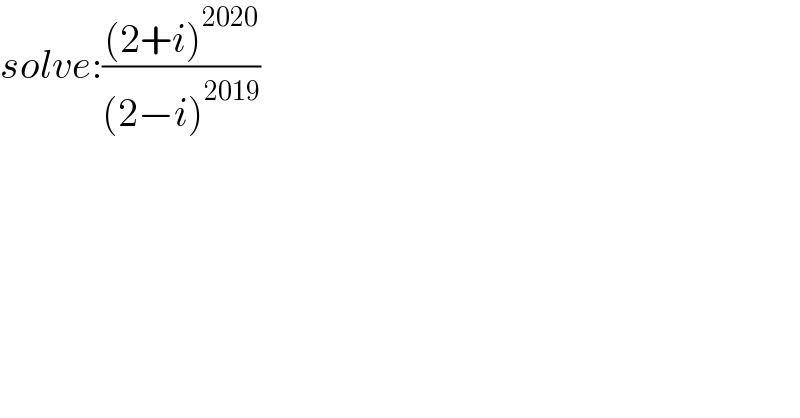
$${solve}:\frac{\left(\mathrm{2}+{i}\right)^{\mathrm{2020}} }{\left(\mathrm{2}−{i}\right)^{\mathrm{2019}} } \\ $$
Answered by Dwaipayan Shikari last updated on 16/Jan/21
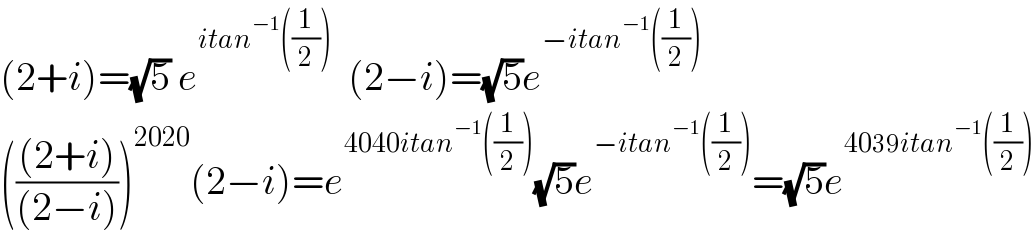
$$\left(\mathrm{2}+{i}\right)=\sqrt{\mathrm{5}}\:{e}^{{itan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\:\left(\mathrm{2}−{i}\right)=\sqrt{\mathrm{5}}{e}^{−{itan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\left(\frac{\left(\mathrm{2}+{i}\right)}{\left(\mathrm{2}−{i}\right)}\right)^{\mathrm{2020}} \left(\mathrm{2}−{i}\right)={e}^{\mathrm{4040}{itan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \sqrt{\mathrm{5}}{e}^{−{itan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)} =\sqrt{\mathrm{5}}{e}^{\mathrm{4039}{itan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$
