Question Number 92013 by I want to learn more last updated on 04/May/20
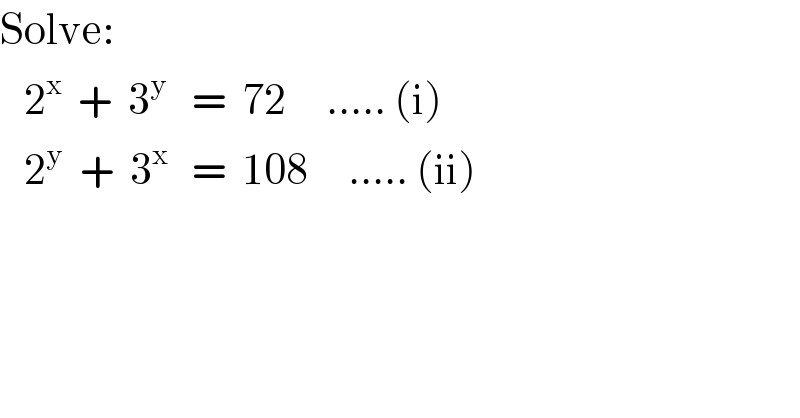
$$\mathrm{Solve}: \\ $$$$\:\:\:\mathrm{2}^{\mathrm{x}} \:\:+\:\:\mathrm{3}^{\mathrm{y}} \:\:\:=\:\:\mathrm{72}\:\:\:\:\:…..\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\mathrm{2}^{\mathrm{y}} \:\:+\:\:\mathrm{3}^{\mathrm{x}} \:\:\:=\:\:\mathrm{108}\:\:\:\:\:…..\:\left(\mathrm{ii}\right) \\ $$
Commented by jagoll last updated on 04/May/20

$$\mathrm{108}×\mathrm{2}=\mathrm{216} \\ $$$$\mathrm{why}\:\mathrm{416}?? \\ $$
Commented by jagoll last updated on 04/May/20

$$\mathrm{x}=\mathrm{y}+\mathrm{2}\: \\ $$$$\mathrm{2}^{\mathrm{y}+\mathrm{2}} +\mathrm{3}^{\mathrm{y}} \:=\:\mathrm{72} \\ $$$$\mathrm{2}^{\mathrm{y}} +\mathrm{3}^{\mathrm{y}+\mathrm{2}} \:=\:\mathrm{108}\: \\ $$$$\mathrm{let}\:\mathrm{2}^{\mathrm{y}} =\mathrm{t}\:\wedge\:\mathrm{3}^{\mathrm{y}} =\mathrm{w} \\ $$$$\mathrm{4t}+\mathrm{w}\:=\:\mathrm{72} \\ $$$$\mathrm{t}+\mathrm{9w}=\mathrm{108}\: \\ $$$$\mathrm{now}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\mathrm{Why}\:\mathrm{do}\:\mathrm{we}\:\mathrm{let}\:\:\:\:\mathrm{x}\:\:=\:\:\mathrm{y}\:+\:\mathrm{2} \\ $$$$\mathrm{can}\:\mathrm{i}\:\mathrm{still}\:\mathrm{say}\:\:\:\:\:\mathrm{x}\:\:=\:\:\mathrm{y}\:\:+\:\:\mathrm{5}\: \\ $$
Commented by jagoll last updated on 04/May/20

$$\mathrm{eq}\left(\mathrm{1}\right)\:×\:\mathrm{by}\:\mathrm{3} \\ $$$$\mathrm{eq}\left(\mathrm{2}\right)\:×\:\mathrm{by}\:\mathrm{2}\: \\ $$$$\mathrm{substract}\:\left(\mathrm{1}\right)\:\&\left(\mathrm{2}\right) \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\:\:\:\:\:\:\mathrm{3}\left(\mathrm{2}^{\mathrm{x}} \right)\:\:+\:\:\mathrm{3}^{\mathrm{y}\:\:+\:\:\mathrm{1}} \:\:\:=\:\:\:\mathrm{216} \\ $$$$\:\:\:\:\:\mathrm{2}^{\mathrm{y}\:+\:\mathrm{1}} \:\:+\:\:\mathrm{2}\left(\mathrm{3}^{\mathrm{x}} \right)\:\:=\:\:\mathrm{216} \\ $$$$\mathrm{Please}\:\mathrm{next}\:\mathrm{step}\:\mathrm{here} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{y}\:+\:\mathrm{1}} \:\:−\:\:\mathrm{3}\left(\mathrm{2}^{\mathrm{x}} \right)\:\:\:+\:\:\mathrm{2}\left(\mathrm{3}^{\mathrm{x}} \right)\:\:−\:\:\mathrm{3}^{\mathrm{y}\:+\:\mathrm{1}} \:\:=\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{2}\left(\mathrm{3}^{\mathrm{x}} \right)\:\:−\:\:\mathrm{3}\left(\mathrm{2}^{\mathrm{x}} \right)\:\:=\:\:\mathrm{3}^{\mathrm{y}\:+\:\mathrm{1}} \:\:−\:\:\mathrm{2}^{\mathrm{y}\:\:+\:\:\mathrm{1}} \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\mathrm{sir},\:\mathrm{show}\:\mathrm{the}\:\mathrm{steps}\:\mathrm{till}\:\mathrm{when}\:\mathrm{you}\:\mathrm{say}\:\mathrm{let}\:\:\mathrm{x}\:=\:\mathrm{y}\:+\:\mathrm{2}. \\ $$$$\mathrm{i}\:\mathrm{will}\:\mathrm{do}\:\mathrm{the}\:\mathrm{rest} \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\mathrm{Have}\:\mathrm{changed}\:\mathrm{it}.\:\mathrm{please}\:\mathrm{next}\:\mathrm{steps}. \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\mathrm{t}\:\:=\:\:\mathrm{15}.\mathrm{429}\:\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{w}\:\:\:=\:\:\:\mathrm{10}.\mathrm{286} \\ $$$$\:\:\:\:\:\mathrm{2}^{\mathrm{y}} \:\:=\:\:\mathrm{15}.\mathrm{429} \\ $$$$\:\:\:\:\:\:\mathrm{y}\:\:=\:\:\frac{\mathrm{ln}\left(\mathrm{15}.\mathrm{429}\right)}{\mathrm{ln}\left(\mathrm{2}\right)}\:\:\:=\:\:\:\frac{\mathrm{2}.\mathrm{736}}{\mathrm{0}.\mathrm{6931}}\:\:\:=\:\:\:\mathrm{3}.\mathrm{9475} \\ $$$$\:\:\:\:\mathrm{x}\:\:\:=\:\:\:\mathrm{3}.\mathrm{9475}\:\:+\:\:\mathrm{2}\:\:\:=\:\:\mathrm{5}.\mathrm{9475} \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{not}\:\mathrm{correct}\:\mathrm{with}\:\mathrm{the}\:\mathrm{question} \\ $$
Commented by MJS last updated on 05/May/20

$${x}={y}+\mathrm{2}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{the}\:\mathrm{path}\:\mathrm{given}\:\mathrm{to}\:\mathrm{get}\:{x}={y}+\mathrm{2}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Answered by MJS last updated on 04/May/20

$$\mathrm{approximating}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}\approx\mathrm{4}.\mathrm{15063} \\ $$$${y}\approx\mathrm{3}.\mathrm{63495} \\ $$
Commented by I want to learn more last updated on 04/May/20

$$\mathrm{But}\:\mathrm{using}\:\mathrm{the}\:\mathrm{approach}\:\mathrm{above},\:\mathrm{am}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{it} \\ $$
