Question Number 16723 by tawa tawa last updated on 25/Jun/17
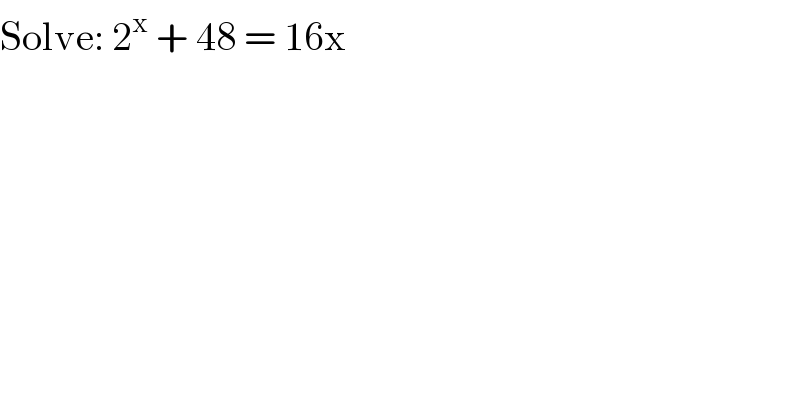
$$\mathrm{Solve}:\:\mathrm{2}^{\mathrm{x}} \:+\:\mathrm{48}\:=\:\mathrm{16x} \\ $$
Answered by mrW1 last updated on 26/Jun/17
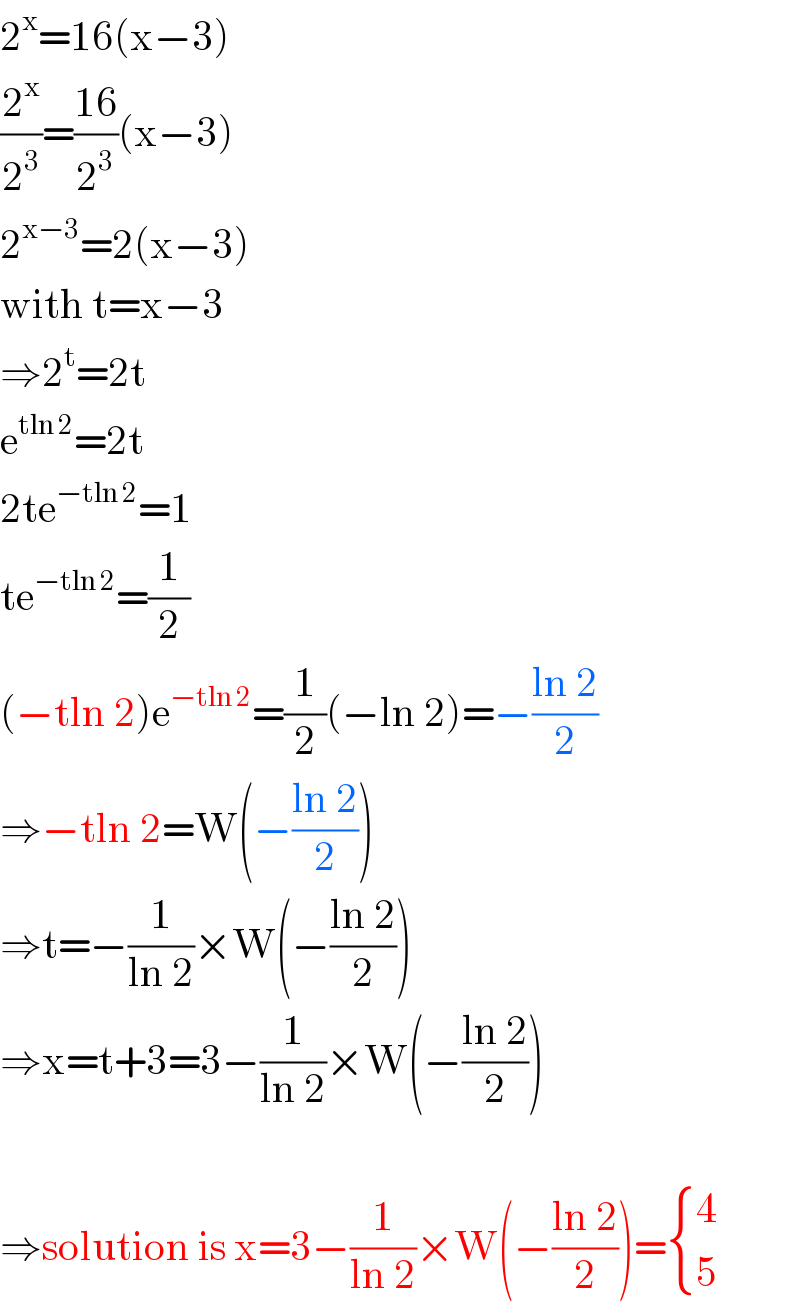
$$\mathrm{2}^{\mathrm{x}} =\mathrm{16}\left(\mathrm{x}−\mathrm{3}\right) \\ $$$$\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{2}^{\mathrm{3}} }=\frac{\mathrm{16}}{\mathrm{2}^{\mathrm{3}} }\left(\mathrm{x}−\mathrm{3}\right) \\ $$$$\mathrm{2}^{\mathrm{x}−\mathrm{3}} =\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right) \\ $$$$\mathrm{with}\:\mathrm{t}=\mathrm{x}−\mathrm{3} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{t}} =\mathrm{2t} \\ $$$$\mathrm{e}^{\mathrm{tln}\:\mathrm{2}} =\mathrm{2t} \\ $$$$\mathrm{2te}^{−\mathrm{tln}\:\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{te}^{−\mathrm{tln}\:\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(−\mathrm{tln}\:\mathrm{2}\right)\mathrm{e}^{−\mathrm{tln}\:\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{ln}\:\mathrm{2}\right)=−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$$\Rightarrow−\mathrm{tln}\:\mathrm{2}=\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{t}=−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}}×\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{t}+\mathrm{3}=\mathrm{3}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}}×\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{solution}\:\mathrm{is}\:\mathrm{x}=\mathrm{3}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}}×\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=\begin{cases}{\mathrm{4}}\\{\mathrm{5}}\end{cases} \\ $$
Commented by tawa tawa last updated on 26/Jun/17

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
