Question Number 113191 by ZiYangLee last updated on 11/Sep/20
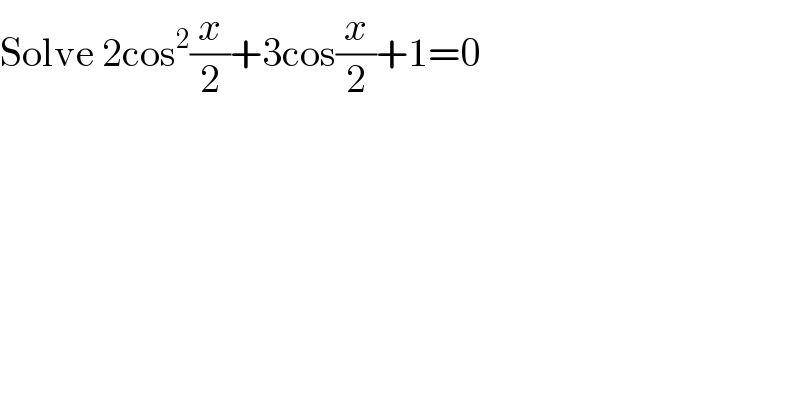
$$\mathrm{Solve}\:\mathrm{2cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{3cos}\frac{{x}}{\mathrm{2}}+\mathrm{1}=\mathrm{0} \\ $$
Answered by bobhans last updated on 11/Sep/20
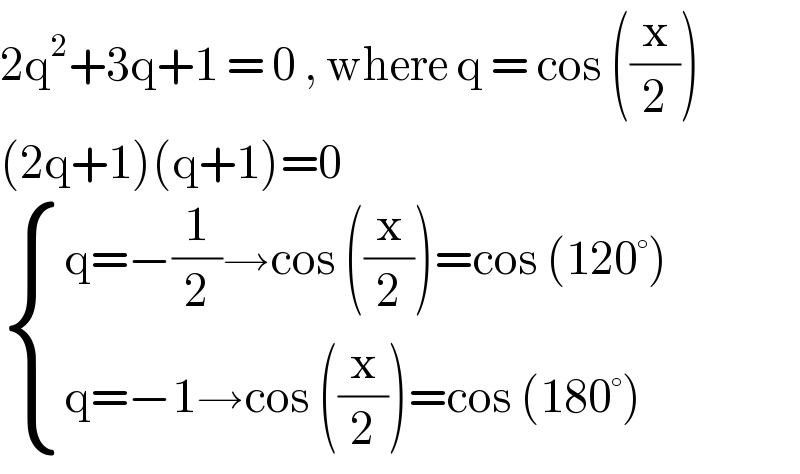
$$\mathrm{2q}^{\mathrm{2}} +\mathrm{3q}+\mathrm{1}\:=\:\mathrm{0}\:,\:\mathrm{where}\:\mathrm{q}\:=\:\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$$$\left(\mathrm{2q}+\mathrm{1}\right)\left(\mathrm{q}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{q}=−\frac{\mathrm{1}}{\mathrm{2}}\rightarrow\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{cos}\:\left(\mathrm{120}°\right)}\\{\mathrm{q}=−\mathrm{1}\rightarrow\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{cos}\:\left(\mathrm{180}°\right)}\end{cases} \\ $$
Commented by ZiYangLee last updated on 11/Sep/20
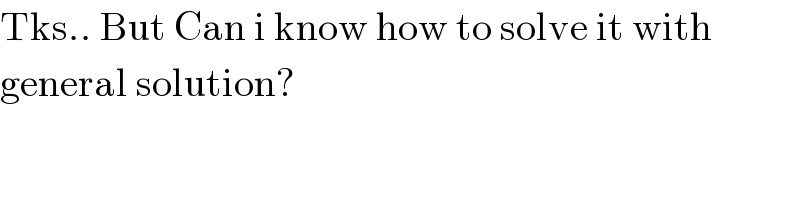
$$\mathrm{Tks}..\:\mathrm{But}\:\mathrm{Can}\:\mathrm{i}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{with}\: \\ $$$$\mathrm{general}\:\mathrm{solution}? \\ $$
Commented by john santu last updated on 11/Sep/20
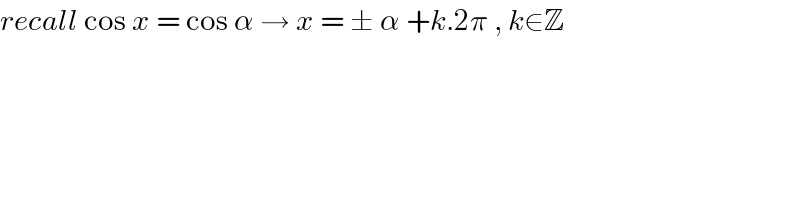
$${recall}\:\mathrm{cos}\:{x}\:=\:\mathrm{cos}\:\alpha\:\rightarrow\:{x}\:=\:\pm\:\alpha\:+{k}.\mathrm{2}\pi\:,\:{k}\in\mathbb{Z} \\ $$
