Question Number 168011 by Mastermind last updated on 31/Mar/22
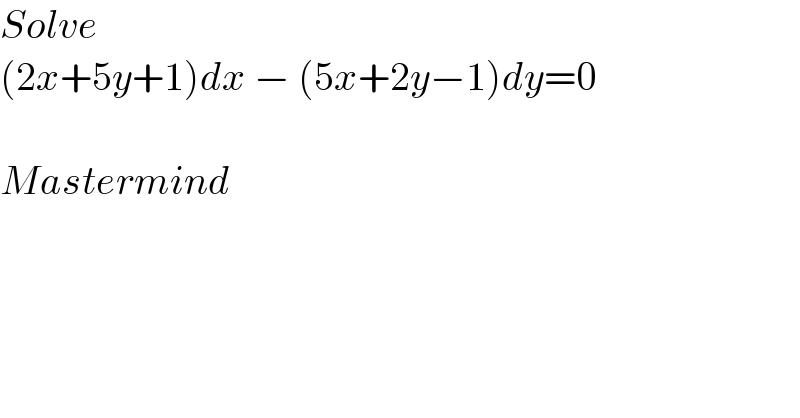
$${Solve}\: \\ $$$$\left(\mathrm{2}{x}+\mathrm{5}{y}+\mathrm{1}\right){dx}\:−\:\left(\mathrm{5}{x}+\mathrm{2}{y}−\mathrm{1}\right){dy}=\mathrm{0} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by mr W last updated on 03/Apr/22
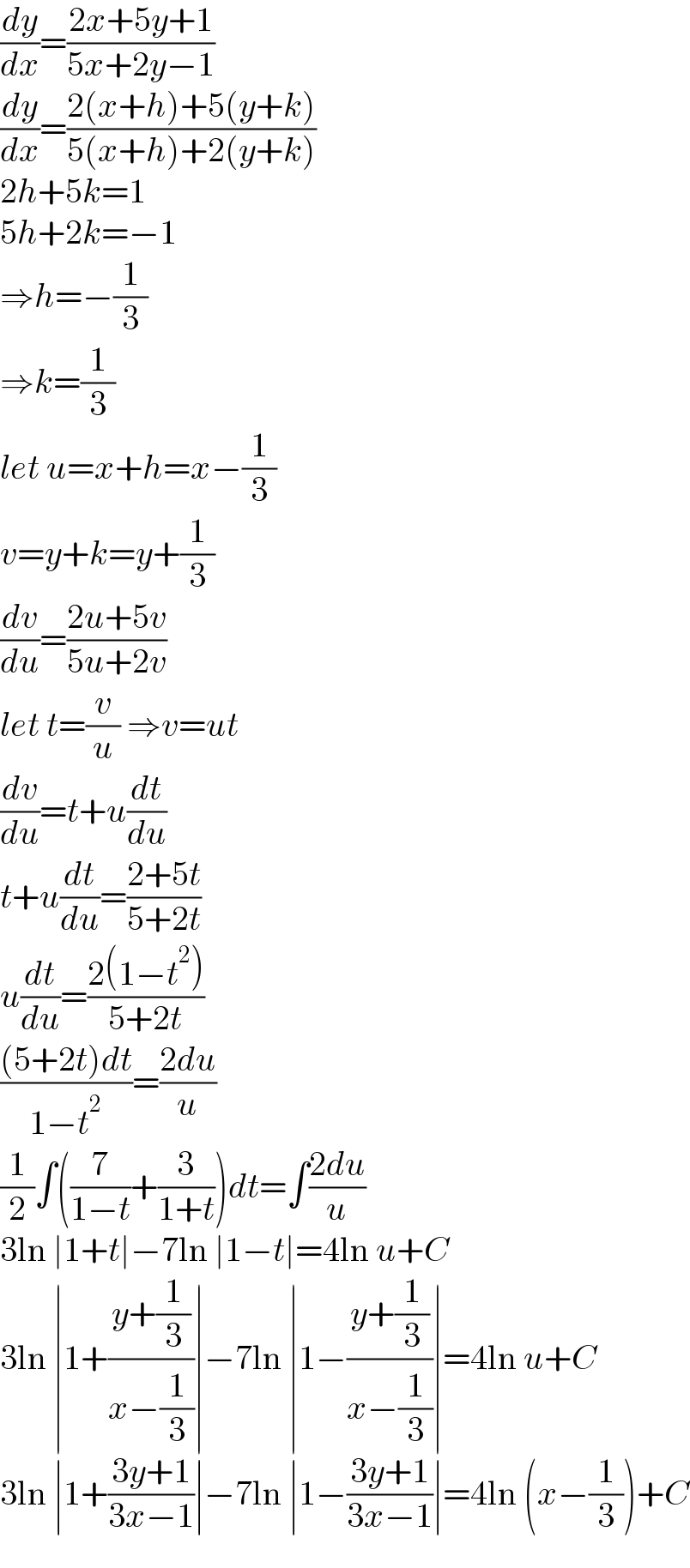
$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}{x}+\mathrm{5}{y}+\mathrm{1}}{\mathrm{5}{x}+\mathrm{2}{y}−\mathrm{1}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}\left({x}+{h}\right)+\mathrm{5}\left({y}+{k}\right)}{\mathrm{5}\left({x}+{h}\right)+\mathrm{2}\left({y}+{k}\right)} \\ $$$$\mathrm{2}{h}+\mathrm{5}{k}=\mathrm{1} \\ $$$$\mathrm{5}{h}+\mathrm{2}{k}=−\mathrm{1} \\ $$$$\Rightarrow{h}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${let}\:{u}={x}+{h}={x}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${v}={y}+{k}={y}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{{dv}}{{du}}=\frac{\mathrm{2}{u}+\mathrm{5}{v}}{\mathrm{5}{u}+\mathrm{2}{v}} \\ $$$${let}\:{t}=\frac{{v}}{{u}}\:\Rightarrow{v}={ut} \\ $$$$\frac{{dv}}{{du}}={t}+{u}\frac{{dt}}{{du}} \\ $$$${t}+{u}\frac{{dt}}{{du}}=\frac{\mathrm{2}+\mathrm{5}{t}}{\mathrm{5}+\mathrm{2}{t}} \\ $$$${u}\frac{{dt}}{{du}}=\frac{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{5}+\mathrm{2}{t}} \\ $$$$\frac{\left(\mathrm{5}+\mathrm{2}{t}\right){dt}}{\mathrm{1}−{t}^{\mathrm{2}} }=\frac{\mathrm{2}{du}}{{u}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{7}}{\mathrm{1}−{t}}+\frac{\mathrm{3}}{\mathrm{1}+{t}}\right){dt}=\int\frac{\mathrm{2}{du}}{{u}} \\ $$$$\mathrm{3ln}\:\mid\mathrm{1}+{t}\mid−\mathrm{7ln}\:\mid\mathrm{1}−{t}\mid=\mathrm{4ln}\:{u}+{C} \\ $$$$\mathrm{3ln}\:\mid\mathrm{1}+\frac{{y}+\frac{\mathrm{1}}{\mathrm{3}}}{{x}−\frac{\mathrm{1}}{\mathrm{3}}}\mid−\mathrm{7ln}\:\mid\mathrm{1}−\frac{{y}+\frac{\mathrm{1}}{\mathrm{3}}}{{x}−\frac{\mathrm{1}}{\mathrm{3}}}\mid=\mathrm{4ln}\:{u}+{C} \\ $$$$\mathrm{3ln}\:\mid\mathrm{1}+\frac{\mathrm{3}{y}+\mathrm{1}}{\mathrm{3}{x}−\mathrm{1}}\mid−\mathrm{7ln}\:\mid\mathrm{1}−\frac{\mathrm{3}{y}+\mathrm{1}}{\mathrm{3}{x}−\mathrm{1}}\mid=\mathrm{4ln}\:\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right)+{C} \\ $$
Commented by Tawa11 last updated on 03/Apr/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Mastermind last updated on 05/Apr/22

$${Thanks}\:{man} \\ $$
Answered by ajfour last updated on 06/Apr/22
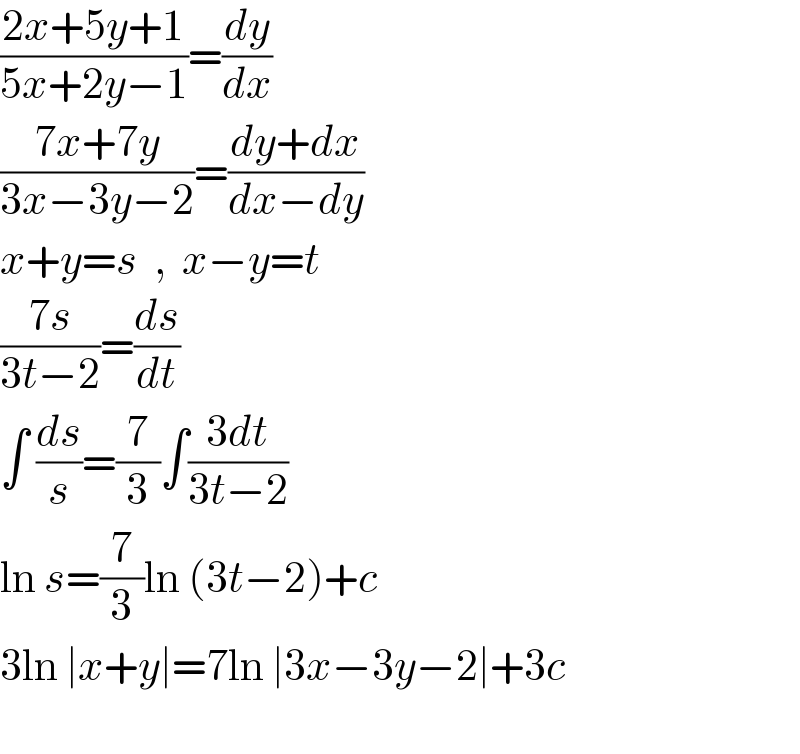
$$\frac{\mathrm{2}{x}+\mathrm{5}{y}+\mathrm{1}}{\mathrm{5}{x}+\mathrm{2}{y}−\mathrm{1}}=\frac{{dy}}{{dx}} \\ $$$$\frac{\mathrm{7}{x}+\mathrm{7}{y}}{\mathrm{3}{x}−\mathrm{3}{y}−\mathrm{2}}=\frac{{dy}+{dx}}{{dx}−{dy}} \\ $$$${x}+{y}={s}\:\:,\:\:{x}−{y}={t} \\ $$$$\frac{\mathrm{7}{s}}{\mathrm{3}{t}−\mathrm{2}}=\frac{{ds}}{{dt}} \\ $$$$\int\:\frac{{ds}}{{s}}=\frac{\mathrm{7}}{\mathrm{3}}\int\frac{\mathrm{3}{dt}}{\mathrm{3}{t}−\mathrm{2}} \\ $$$$\mathrm{ln}\:{s}=\frac{\mathrm{7}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{3}{t}−\mathrm{2}\right)+{c} \\ $$$$\mathrm{3ln}\:\mid{x}+{y}\mid=\mathrm{7ln}\:\mid\mathrm{3}{x}−\mathrm{3}{y}−\mathrm{2}\mid+\mathrm{3}{c} \\ $$$$ \\ $$
Commented by mr W last updated on 08/Apr/22

$${nice}\:{solution}! \\ $$
